En Ciencias de la Salud es frecuente encontrar variables cualitativas o categóricas donde los datos se pueden expresar como proporciones o porcentajes de valores determinados de la variable en dos o más grupos de pacientes. Este análisis equivale al contraste de dos variables con escala de medida nominal; por ejemplo, proporción de pacientes que precisan ingreso (sí o no) en función del tipo de tratamiento recibido (por ejemplo, tratamiento o placebo). El contraste de hipótesis más utilizado para analizar la relación entre estas variables se basa en la prueba de la Ji-cuadrado de Pearson (χ²), que compara la divergencia entre los porcentajes observados y los esperados bajo el supuesto de la hipótesis nula de igualdad. Es aplicable tanto a las variables nominales dicotómicas como a las politómicas no ordinales. Tiene la particularidad de que el contraste es siempre bilateral, la hipótesis nula (H_o) es la igualdad de la distribución de los datos en las dos variables y la alternativa (H₁) es la ausencia de igualdad. Este mismo test puede emplearse para comparar un porcentaje respecto a un valor teórico.

Para la comparación de proporciones podemos utilizar, además de la χ², otras pruebas de contraste, como las pruebas z, aplicables a muestras con suficiente tamaño muestral como para emplear la aproximación de la distribución binomial a la normal, y para cualquier circunstancia, pruebas exactas, basadas en la distribución binomial.

Prueba de comparación de dos o más proporciones

1. Prueba χ²

Clásicamente se diferencian en pruebas de homogeneidad y de independencia, diferenciables desde el punto de vista epidemiológico, ya que estadísticamente el fundamento es el mismo:

• Prueba de homogeneidad. Trata de comprobar si una variable cualitativa se distribuye de manera similar en dos o más muestras diferentes. Se emplea en estudios de cohortes y de casos y controles, en los que las muestras se diferencian por un valor diferente de la variable de exposición o de respuesta, respectivamente, y se quiere saber si las muestras son homogéneas en cuanto a la variable cualitativa, que será según el tipo de estudio, de respuesta o de exposición. Ejemplo: con el objetivo de evaluar si el tabaquismo es un factor de riesgo de bajo peso al nacimiento en los recién nacidos, se seleccionan dos muestras aleatorias, una con embarazadas fumadoras y otra no fumadoras, y se analiza el porcentaje de recién nacidos de bajo peso en ambas muestras para ver si es similar o, por el contrario, distinta en el grupo de fumadoras.
• Prueba de independencia. Trata de explorar si en una muestra de individuos los valores de dos variables están asociadas o son independientes. Se utiliza en los diseños transversales. Un ejemplo clásico es el estudio de la relación entre el color del cabello (rubio/negro) y los ojos (azules/marrones). Se trata de conocer si ambas categorías se distribuyen de igual forma en las dos variables.

Para comprender la mecánica de la prueba χ², la ilustraremos con un ejemplo. En un estudio de cohortes ficticio, se investiga si el ambiente tabáquico en el domicilio (variable: tabaquismo) es un factor de riesgo de ingreso hospitalario (variable: Ing_asma) en los pacientes asmáticos. Para ello hemos seleccionado 30 asmáticos, 16 expuestos al tabaco (16/30 = 53,3%) y 14 no expuestos (14/30 = 46,7%). Supongamos que obtenemos los siguientes resultados: de los 16 expuestos ingresan en el hospital 14 (87,5%) y de los 14 no expuestos ingresan 3 (21,4%). Se trata de saber si la variable ingreso hospitalario se distribuye de distinta forma entre los expuestos al tabaco y no expuestos al tabaco.

Para ello, lo mejor es hacerlo por pasos:

1. Comprobar el tipo de variables y la prueba estadística a utilizar. Se trata de dos variables nominales dicotómicas que podemos codificar como tabaquismo (sí/no), ingreso hospitalario (sí/no) y la prueba estadística pertinente es la χ².
2. Construcción de la tabla de contingencia. Llamada también tabla 2 × 2 o de doble entrada, en caso de dos variables. Colocamos en una entrada (filas) la variable de exposición (tabaquismo) y en la otra entrada (columnas) la variable resultado (Ing_asma) y rellenamos las cuatro casillas con los resultados obtenidos o valores observados (tabla 1).

Tabla 1. Tabla de contingencia entre tabaquismo e ingreso por asma. Mostrar/ocultar

Tabla 1. Tabla de contingencia entre tabaquismo e ingreso por asma
	Ingreso por asma
Tabaquismo	No	Sí	Total
No	11	3	14
Sí	2	14	16
Total	13	17	30

3. Plantear el contraste de hipótesis. Se trata de un contraste bilateral donde la hipótesis nula es que las dos muestras sean homogéneas y la hipótesis alternativa la heterogeneidad de las mismas. En nuestro ejemplo la hipótesis nula (H₀) será que la proporción de ingresos (p) es igual en los dos grupos, o sea, que el ingreso por asma no está asociado al tabaquismo familiar. La hipótesis alternativa será que las proporciones de ingresos son distintas en los dos grupos. La formulación de las hipótesis se realiza de la siguiente manera:

Hipótesis nula (H0)⋮ π ingresos por tabaquismo = π ingresos por no tabaquismo.

Hipótesis alternativa (H1)⋮ π ingresos por tabaquismo ≠ π ingresos por no tabaquismo.

4. Calcular los valores esperados. Para calcular los valores esperados utilizamos los valores totales o marginales (suma de los valores de cada fila o columna), multiplicando el número de observados de la fila por el número total de observados de las columnas dividiéndola por el total de los totales observados.

Valor esperado = (n.º total observados fila) × (n.º total observados columna) / n.º total de observados.

Ejemplo: calculemos el valor esperado de los que ingresan por asma y no presentan antecedentes de tabaquismo familiar. Esperados_{casos expuestos} = 14 × 17 / 30 = 7,93. Y así sucesivamente calculamos todos (tabla 2).

Tabla 2. Valores observados y esperados. Mostrar/ocultar

Tabla 2. Valores observados y esperados
		Ing_asma
Tabaquismo		No	Sí	Total
No	Observados	11	3	14
	Esperados	6,07	7,93	14
Sí	Observados	2	14	16
	Esperados	6,93	9,07	16
Total	Observados	13	17	30
	Esperados	13	17	30

5. Calcular el valor de la χ². La prueba de χ² se basa en comparar los valores de los datos observados con los esperados en cada casilla. Para que las diferencias positivas no se anulen con las negativas, se elevan al cuadrado estas diferencias y se dividen por las frecuencias esperadas. La distribución de χ² refleja la probabilidad de los valores de χ² calculados con todos los recuentos observados posibles en cada casilla (de 0 al tamaño muestral). Cuanto más se parezca el valor observado al esperado, χ² será menor, cuanto más se diferencien χ² será mayor. En función del número de casillas de la tabla de contingencia la distribución χ² cambia con lo que denominamos grados de libertad. Cuánto mayor sea el valor de la χ² menor probabilidad habrá de que ocurra el suceso y si esa probabilidad es lo suficiente baja (<0,05), podremos decir que los ingresos por asma en los que tienen tabaquismo se distribuyen de forma distinta que en los que no tienen tabaquismo. Aplicando la ecuación χ²:

$$X^2 = \sum (\frac {(observados - esperados)^2}{esperados})$$

Obtenemos:

$$ X^2 = \sum (\frac {(observados - esperados)^2}{esperados})= \frac {(11-6,07)^2}{6,07} + \frac {(3-7,93)^2}{7,93} + \frac {(2-6,93)^2}{6,93} + \frac {(14-9,07)^2}{9,07} = 13,27.$$

El valor de la χ² exp (experimental) = 13,27.

6. Calcular los grados de libertad (gl). Para una tabla 2 × 2 donde los marginales son fijos, introduciendo solo un valor en las casillas quedan los otros tres determinados, en nuestro caso presenta 1 grado de libertad. En general se puede decir que: gl = (n.º columnas - 1) × (n.º filas - 1).
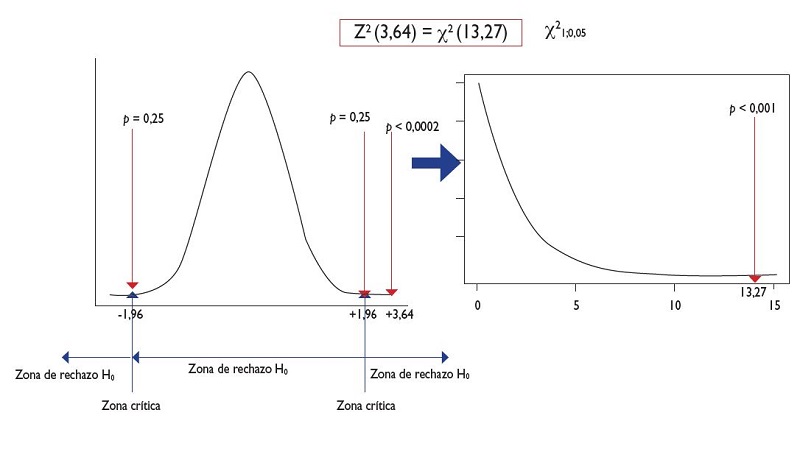
7. Calcular la probabilidad del valor de la χ² obtenida (valor de p). El valor de la χ² t (teórico) con un grado de libertad que le corresponde una p = 0,05 es de 3,84 (χ²_1;0,05 = 3,84), esta es la zona crítica de rechazo y cualquier valor menor que este a la izquierda queda en la zona de no rechazo de la hipótesis nula, con un valor de p >0,05, siendo por tanto un valor estadísticamente no significativo. El valor de la χ² exp = 13,27 es mayor que la χ² critica (χ²_1;0,05 = 3,84), quedando por tanto en la zona de rechazo de la hipótesis nula. Consultando en las tablas de distribución de la χ² con gl = 1¹, vemos que el valor mínimo más cercano que encontramos es χ²_1;0,001 = 10,82, como el valor de nuestra χ² exp es mayor que 10,82 interpretamos que la probabilidad de rechazo es menor que 0,001 (p <0,001). El valor exacto lo conoceremos posteriormente cuando realicemos la prueba mediante el programa estadístico (figura 1).

Figura 1. Distribución χ² con gl=1. Prueba comparación de dos proporciones entre Tabaquismo/ingreso por asma. Mostrar/ocultar


8. Obtener la conclusión. El valor de p obtenido (p <0,001), es lo suficientemente pequeño (<0,05) para rechazar la hipótesis nula de igualdad de las proporciones de ingresos por asma en los dos grupos. Podremos concluir que existe asociación estadísticamente significativa (p <0,001) entre el tabaquismo familiar y el ingreso por asma en pacientes asmáticos.
9. Comprobar los requisitos de aplicación. Existen dos condiciones de aplicación:
   1. Las dos variables deben ser en escala nominal (no ordinal).
   2. Ninguno de los valores esperados debe ser menor de 5 (para tablas con más de cuatro casillas menos del 20% de los valores esperados).

   En nuestro caso se cumplen las dos condiciones, las dos variables son nominales y el valor esperado más pequeño es de 6,07. Cuando no se cumplen estos requisitos hay que recurrir a las pruebas exactas o de aproximación.

Pruebas exactas y de aproximación

En las muestras pequeñas, es común que no se cumplan las condiciones de aplicación de la Ji-cuadrado (número de valores esperados sea mayor de 5 en menos del 20% de las casillas), la solución es emplear métodos exactos o aproximados.

• Métodos exactos. La prueba exacta de Fisher consiste en usar la distribución binomial para conocer la probabilidad exacta de que ocurra el suceso. El p valor obtenido es más conservador (más elevado), lo que ofrece mayor seguridad si es significativo.
• Métodos aproximados. La corrección por continuidad de Yates se basa en disminuir 0,5 el valor absoluto de las diferencias observadas y esperadas, el numerador del estadístico χ². Al igual que la prueba de Fisher se obtiene un p valor más conservador, pero menos real.
• Nuestro consejo es, en muestras pequeñas, utilizar la prueba exacta de Fisher, porque es el más conservador y se acerca más a la realidad².

Aunque hemos visto que el cálculo es relativamente sencillo, aconsejamos utilizar un programa estadístico. Veamos el ejemplo utilizando un programa de acceso libre, el software estadístico R (https://www.r-project.org/) con el plugin RCommander. Si necesita saber cómo instalar RCommander, puede consultar el siguiente tutorial en línea (http://sct.uab.cat/estadistica/sites/sct.uab.cat.estadistica/files/instalacion_r_commander_0.pdf).

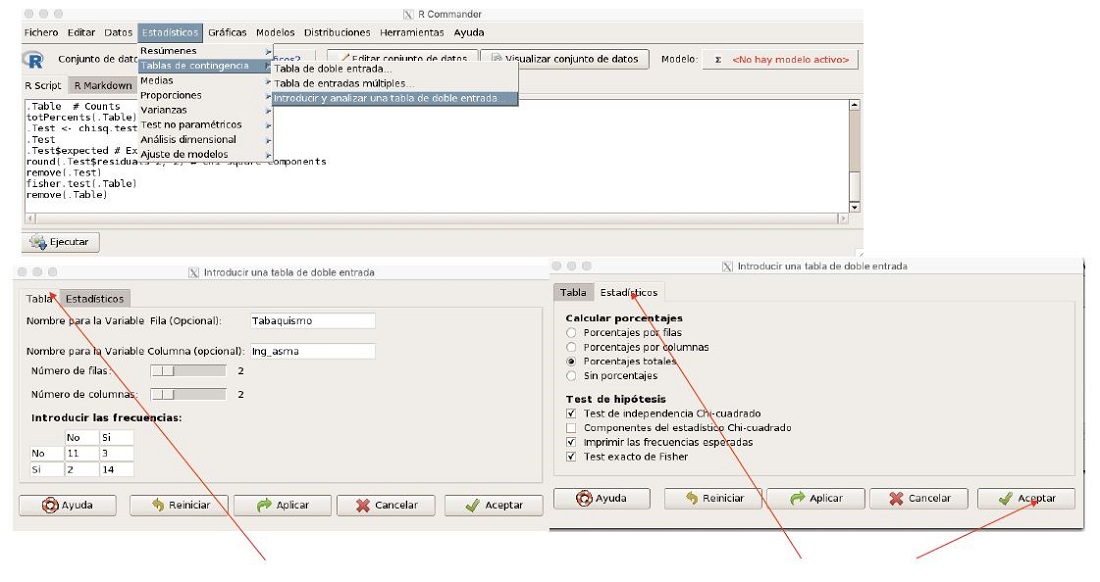
Abrimos RCommander, nos vamos al menú de opciones seleccionamos estadísticos → tablas de contingencia → tablas de doble entrada. En la pestaña tabla introducimos el nombre de la variable en la fila = tabaquismo y el nombre de la variable en la columna = ing_asma. En el número de filas y columnas seleccionamos 2. A continuación introducimos la tabla 2 × 2 de frecuencias. En pestaña estadísticos seleccionamos porcentajes totales y en test de hipótesis test independencia χ², imprimir las frecuencias esperadas, test exacto de Fisher y clicamos en aceptar (figura 2).

Figura 2. Tabla de contingencia en Rcommander. Mostrar/ocultar

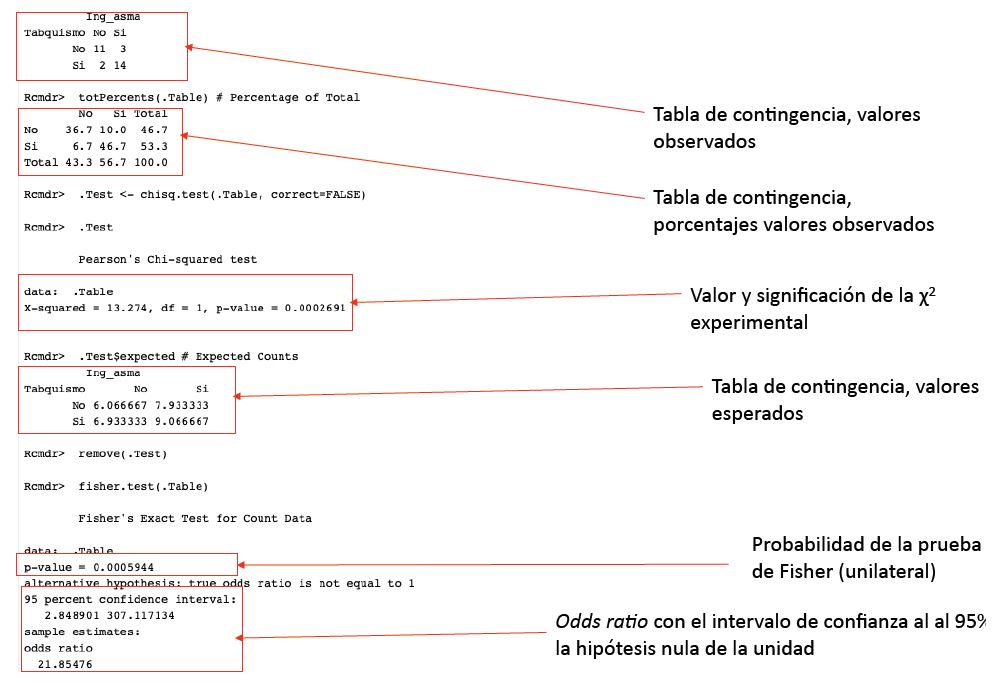
En la ventana de resultados, R nos muestra la tabla de contingencia con los porcentajes totales, El valor de la χ² con un grado de libertad (df = 1) y la probabilidad exacta (χ² = 13,274, df = 1, valor p = 0,0002691). A continuación, los valores esperados, donde podemos comprobar que el valor mínimo coincide con el que hicimos manualmente (6,06). El valor de la prueba exacta de Fisher unilateral (p-value = 0,0005944) bilateral (p = 0,0011), en el que podemos observar que es más conservador que la probabilidad exacta, en nuestro ejemplo, como se cumplen los requisitos de la prueba podemos obviarlo. Por último, se nos muestra el resultado de la odds ratio (OR) con el intervalo de confianza al 95% y el contraste de hipótesis bajo la hipótesis nula OR = 1 (figura 3).

Figura 3. Ventana de resultados de RCommader. Mostrar/ocultar

2. Prueba z para comparación de dos proporciones

En caso de muestras grandes la comparación entre dos proporciones puede realizarse mediante la aproximación de la distribución muestral de la diferencia de las dos proporciones a una distribución normal estandarizada de media 0 y desviación estándar 1 [N(0:1)]. Se acepta como muestra “suficientemente grande” si se cumple que el valor de los esperados es ≥5, esto es igual a multiplicar la proporción total o marginal de ambos grupos y su complementario por el tamaño muestral de cada grupo. Tomemos el ejemplo anterior sobre la relación entre tabaquismo e ingreso hospitalario. Los pasos son los siguientes:

1. Comprobar las condiciones de la aplicación. Recordemos que en nuestro ejemplo (tabla 3) la probabilidad total marginal (p) se calcula dividiendo el total de ingresos por el total de la muestra (17 / 30 = 0,56). El complementario q (1 - 0,56 = 0,44). Los tamaños muestrales son de 14 (grupo no tabaquismo = na) y 16 (grupo tabaquismo = nb). Multiplicando p y q por los tamaños muestrales, obtenemos:

p × na = 0,56 × 14= 7,84; q × na = 0,44 × 14= 6,16; p × nb = 0,56 × 16= 8,96; q × nb=7,04, todos ≥ 5, luego se cumplen las condiciones.

2. Realizar el contraste de hipótesis. Realizamos un contraste bilateral, dónde la hipótesis nula (H₀) sería que no existen diferencias (d) entre la proporción de ingresos en los expuestos al tabaco (p₁) y entre los no expuestos al tabaco (p₂), lo que equivale a decir que la diferencia de proporciones no es distinta de 0; la hipótesis alternativa H₁ es que existen diferencias.

H₀⋮ p₁-p₂ = 0.

H₁⋮ p₁-p₂ ≠0.

3. Obtener el estadístico de contraste. La prueba z se fundamenta en dividir el efecto entre su error. En nuestro caso el efecto es las diferencias de proporciones (d) y el error es el error estándar (EE) de una diferencia de proporciones. La varianza de una diferencia es igual a la suma de las varianzas de cada parte de las diferencias. El EE de la diferencia de proporciones (EEdp) es la raíz cuadrada de la suma de las varianzas divididas, cada una, por su tamaño muestral (n_a,n_b):

$$EEdp = \sqrt {\frac {(p_1\space x\space q_1)}{n_a} + \frac {(p_2\space x\space q_2)}{n_b}}$$$$

$$z = \frac {d}{EEdp} = \frac {p_1 - p_2}{\sqrt {\frac{p_1\space x\space q_1}{n_a} + \frac{p_2\space x\space q_2}{n_b}}} = \frac {0,875 - 0,214}{\sqrt {\frac{p_1\space x\space q_1}{14} + \frac {p_2\space x\space q_2}{16}}} = \frac {0,661}{\sqrt {\frac{p_1\space x\space q_1}{14} + \frac{p_2\space x\space q_2}{16}}} = \frac {0,661}{0,1816} =3,639$$

4. Cálculo del grado de significación. El valor crítico (p = 0,05) de rechazo bilateral de una distribución normal tipificada: N(0:1) es de 1,96, dejando 0,025% de probabilidad más allá de esta zona (zona de rechazo) en cada cola (figura 4). Luego todo valor de z a la izquierda o derecha de ±1,96, caerá en la zona de rechazo y por tanto con una probabilidad <0,05. El lector puede comprobar que el valor de z² coincide con el χ²_gl=1. En nuestro caso z² = 3,63² = 13,17, muy parecido al obtenido anteriormente con la prueba χ² = 13,27. Calculamos la probabilidad en una tabla de distribución normal estandarizada (z_0;1). El valor más cercano es z(_a/2) = 3,59 (p = 0,0002) unilateral. Cómo 3,64 es >3,59 el p valor sería <0,0002, y multiplicando por 2 conocemos el valor bilateral (p <0,0004).

Figura 4. Equivalencia Distribución Normal y χ². Mostrar/ocultar


5. Conclusión de la prueba de significación. Con una significación p <0,0004 podemos decir que los ingresos por asma en el grupo de asmáticos expuestos al tabaco es diferente al del grupo de no expuestos. Como los menús de RCommander, no pueden estimar directamente la p en la prueba z para dos proporciones, haremos los cálculos del ejemplo con otro programa de acceso libre, Epidat 4.2 disponible en (https://www.sergas.es/Saude-publica/EPIDAT-4-2?idioma=es).

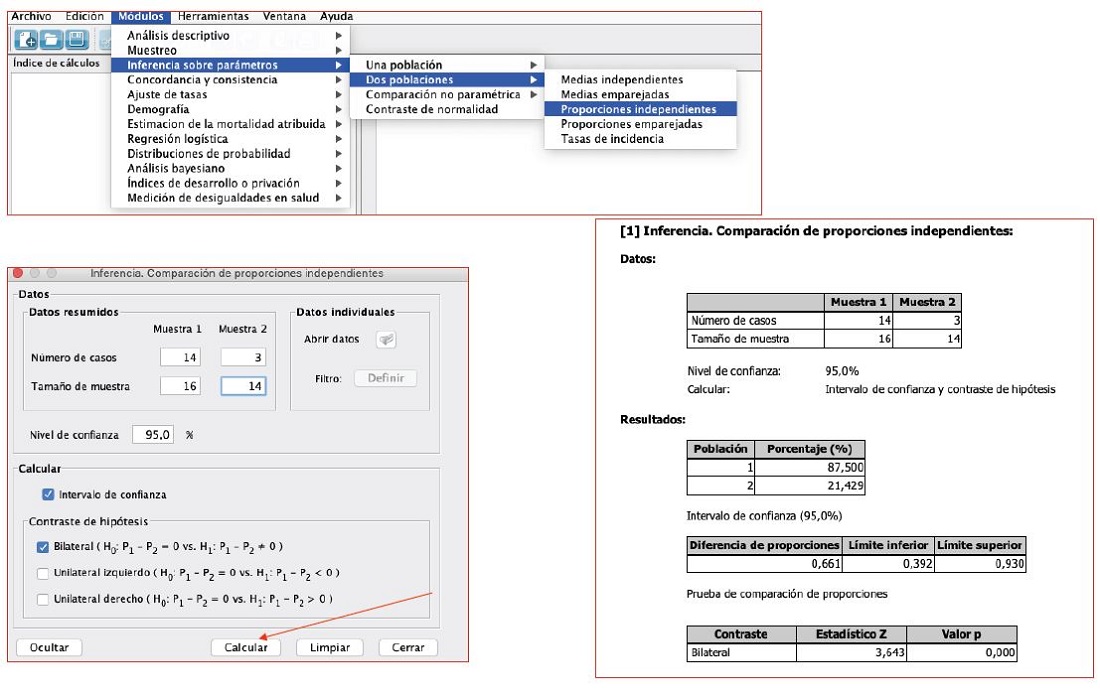
Una vez abierto Epidat, vamos a la pestaña de módulos → inferencia sobre parámetros → dos poblaciones → proporciones independientes. Se nos abre un cuadro de diálogo en el que introducimos el número de casos y el tamaño de muestra, elegimos el nivel de confianza (95%), intervalo de confianza y contraste de hipótesis bilateral y clicamos en calcular. En la ventana de resultados obtenemos: la tabla con el número de casos y el tamaño muestral, las proporciones de los dos grupos (0,875, 0,214), la diferencia de proporciones (0,661), el valor z (3,64) y el nivel de significación (p = 0,0000). Este valor de p debe interpretarse como p <0,001, ya que Epidat no ofrece resultados de más de cuatro decimales. Para terminar, nos ofrece un dato más, que es el intervalo de confianza al 95% (IC 95) de la diferencia de proporciones que nos puede servir también para ver su significación estadística, y en este caso como no incluye el valor 0 rechazamos la hipótesis de nula de igualdad de proporciones (IC 95: 0,392 a 0,93) (figura 5).

Figura 5. Prueba z para diferencias de proporciones. Mostrar/ocultar

Prueba para una proporción. Prueba de χ² de bondad de ajuste o confirmación

Se utiliza cuando en una muestra aleatoria de sujetos queremos conocer si la distribución de los datos observada se ajusta a una distribución teórica conocida. Como se mencionó anteriormente podemos usar el test de χ².

En un estudio transversal ficticio realizado en asmáticos se encontró que la prevalencia del sexo femenino fue del 60% y el masculino del 40%. Se trata de conocer si la distribución observada del sexo femenino está de acuerdo con la teórica del 50% en la población general.

El contraste de hipótesis sería: hipótesis nula (H₀) la proporción (p) esperada de sexo femenino (0,5) será igual a la observada (0,6), por tanto, la hipótesis alternativa será que las proporción esperada y observada serán distintas.

Hipótesis nula (H₀)⋮ π _esperada (0,6) = π _observada (0,5).

Hipótesis alternativa (H₁)⋮ π _esperada (0,6) ≭ π _observada (0,5).

Veamos el ejemplo utilizando R y la base de datos Fundamentos_graficos.RData, disponible en la web de Evidencias en Pediatría.

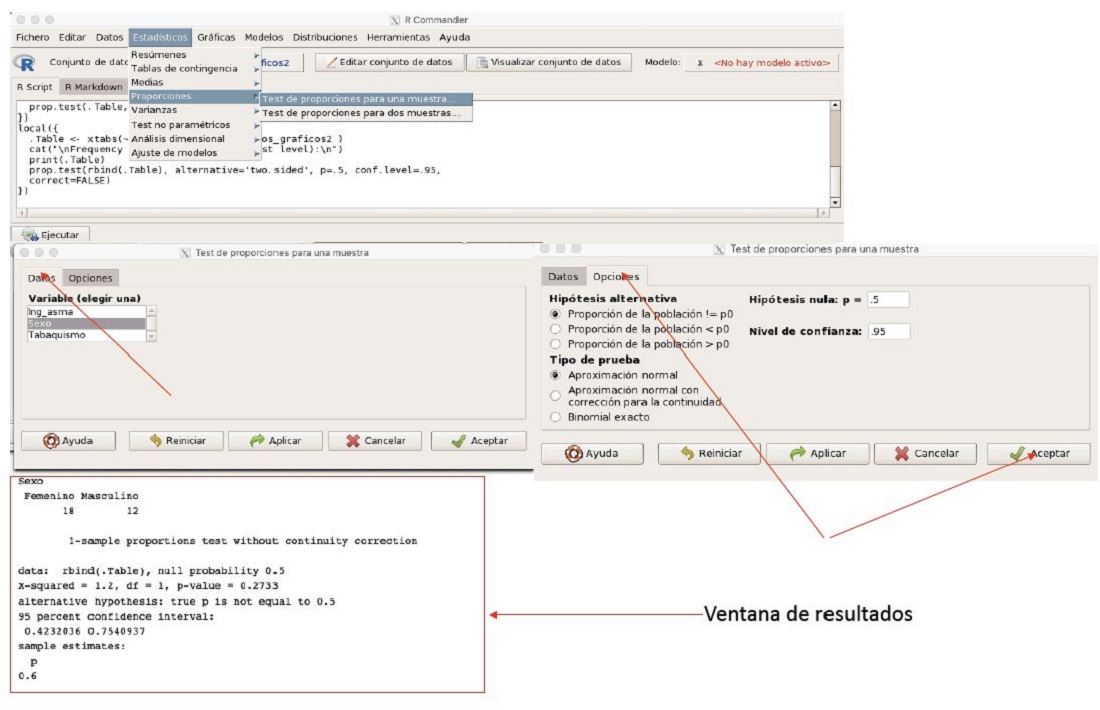
Abrimos RCommander. Una vez cargada la base de datos, nos vamos al menú de opciones y seleccionamos estadísticos → proporciones → test de proporciones de una muestra. En la pestaña datos elegimos la variable Sexo. En opciones elegimos en hipótesis alternativa proporción de las poblaciones iguales, en tipo de prueba aproximación a la normal (es el modo que tiene R de realizar una χ²), en hipótesis nula p = 0,5 y en intervalo de confianza 0,95 y seleccionamos aceptar. En la ventana de resultados se muestra las frecuencias observadas, la prueba que se ha realizado para una muestra (lo que equivale a test de bondad de ajuste), la hipótesis nula = 0,5 y el valor de la χ² con su probabilidad (χ² = 1,2, df = 1, valor de p = 0,2733) sin corrección de continuidad, el intervalo de confianza al 95% de la proporción esperada (figura 6). El lector puede comprobar que, si en la pestaña de opciones elegimos aproximación normal con continuidad de Yates y binomial exacto, obtenemos el valor por corrección de continuidad de Yates (p = 0,3613) y el de la prueba exacta de Fisher unilateral (p = 0,3616), ambos valores más conservadores que el valor de p obtenido con la prueba χ² (figura 6).

Figura 6. Prueba de Bondad de ajuste de la variable sexo en Rcommander. Mostrar/ocultar

Podemos comprobar que se cumplen las condiciones de aplicación de la prueba:

• La variable debe estar en escala nominal.
• Ninguno de los valores esperados debe ser menor de 5. La variable sexo es categórica y la frecuencia mínima esperada es de 15.

Conclusión: el valor de p obtenido (0,273), es lo suficientemente grande (p>0,05) para no poder rechazar la hipótesis nula de que la proporción de individuos del sexo femenino en el estudio es igual a la de la población general.

Bibliografía

• Arriaza Gómez AJ, Fernández Palacín F, López Sánchez MA, Muñoz Márquez M, Pérez Plaza S, Sánchez Navas S. Estadística Básica con R y R–Commander. Cádiz: UCA, 2008.
• Doménech Massons JM. Métodos estadísticos en ciencias de la salud. Unidad didáctica 9: Comparación de proporciones. Medidas de riesgo. Barcelona: Signo; 1998.
• Doménech Massons JM. Métodos estadísticos en ciencias de la salud. Unidad didáctica 10: Relación entre dos variables categóricas. Pruebas χ². Barcelona: Signo; 1998.
• Martínez González MA, Sánchez-Villegas A, Toledo Atucha E, Faulin Fajardo J. Bioestadística amigable. 3.ª edición. Barcelona: Elsevier; 2014.
• Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Inferencia estadística: probabilidad, variables aleatorias y distribuciones de probabilidad. Evid Pediatr. 2019;15:27.
• Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Inferencia estadística: contraste de hipótesis. Evid Pediatr. 2020;16:11.
• Sentís J, Pardell H, Cobo E, Canela J. Manual de Bioestadística. 2.ª edición. Barcelona: Masson; 1995.

Cómo citar este artículo

Ortega Páez E, Ochoa Sangrador C, Molina Arias M. Comparación de proporciones. Pruebas de χ². Evid Pediatr. 2020;16:38.