En artículos previos de esta serie hemos presentado los fundamentos de la estimación por intervalos y del contraste de hipótesis. Debemos recordar que, para cualquiera de esos procesos, hemos de recurrir a muestras poblacionales; si las muestras han sido seleccionadas de forma aleatoria y son suficientemente grandes, los resultados van a ser representativos de lo que ocurre en la población, pero siempre van a tener cierto grado de error por imprecisión, que será inversamente proporcional al tamaño muestral. Por ello, resulta crucial antes de realizar un estudio estimar el número de sujetos que tenemos que reclutar, si queremos conseguir una suficiente precisión.

Estimación del tamaño muestral

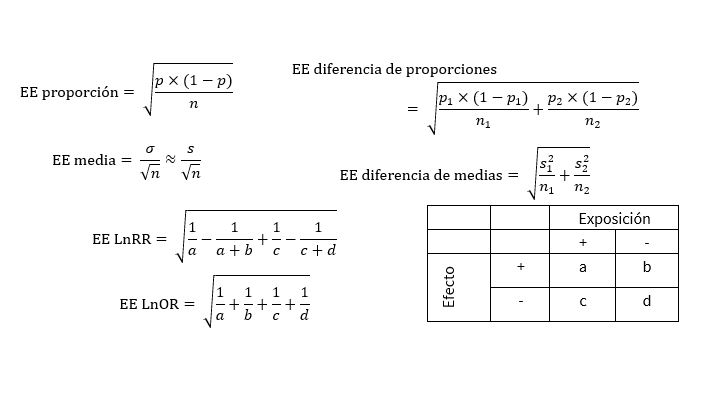
Hemos visto hasta ahora que el estadístico fundamental para estimar parámetros poblacionales o realizar contrastes de hipótesis, cuando recurrimos a distribuciones de probabilidad conocidas, es el error estándar. Recordaremos que, para calcular el error estándar, utilizábamos distintas medidas descriptivas extraídas de la muestra de estudio. Podemos comprobar que en todas las fórmulas de los distintos errores estándar (figura 1) se encontraba el tamaño de la muestra o muestras de estudio.

Figura 1. Fórmulas de estimación de errores estándar de algunos parámetros. Mostrar/ocultar

EE: error estándar; LnRR: logaritmo neperiano del riesgo relativo; LnOR: logaritmo neperiano de la odds ratio; n: tamaño muestral; p: proporción; s: desviación típica muestral; σ: desviación típica poblacional (se estima a partir de s).

Hasta el momento, habíamos recorrido un proceso en el que partíamos del tamaño muestral y otros parámetros descriptivos para obtener la precisión del intervalo de confianza o la probabilidad del contraste de hipótesis. Ahora lo que queremos es realizar el camino inverso, partiendo de una precisión esperada: estimar qué tamaño muestral necesitamos. Si establecemos a priori un intervalo de precisión con el que queremos estimar nuestro parámetro poblacional, podemos calcular el tamaño muestral necesario para ello. Nos basta con despejar de la fórmula correspondiente el tamaño muestral. Así, para la estimación de un porcentaje, se puede despejar n:

$$\ EE\space = \sqrt {{\frac{p *(1-p)}{n}}} ; n\space = {\frac{p *(1-p)}{EE^2}}$$

Si sustituimos en la fórmula el error estándar por la precisión o diferencia (d) buscada (cada uno de los dos lados del intervalo de confianza, ±Z_α/2 x EE, para un intervalo del 95% 1,96 x EE) dividida por Z_α/2 (EE= d/Z_α/2), la fórmula quedaría:

$$\ n\space ≈ {\frac{Z^2_{α/2} * p * (1-p)}{d^2}},$$

siendo d la precisión o diferencia (d = Z_α/2 x EE; siendo Z_α/2 habitualmente 1,96).

Esta fórmula es aproximada, ya que, para simplificarla, hemos ignorado la corrección necesaria cuando la población de muestreo es finita. No obstante, la fórmula solo la presentamos para explicar el fundamento del cálculo de tamaño muestral. En la práctica recurriremos a calculadoras epidemiológicas para realizar las estimaciones.

Por lo tanto, para calcular el tamaño muestral de una proporción solo vamos a necesitar:

• La proporción esperada.
• La precisión de nuestra estimación o diferencia a estimar.

Cuando el parámetro a estimar es una media, en vez de la proporción esperada, tendremos que saber la desviación típica de la característica medida, ya que aparece en la fórmula del error estándar correspondiente. Para otros parámetros, como la diferencia de proporciones, la diferencia de medias, riesgos relativos, odds ratio, etc., hay otros elementos a considerar que van a aparecer en las fórmulas.

Pero ¿de dónde obtenemos la información necesaria? Veamos cómo hacerlo para la estimación de una proporción. Lo primero es establecer la proporción esperada. Para ello, podemos recurrir a nuestro conocimiento previo sobre el objeto de estudio o buscar datos en la literatura científica publicada. Cuando no tenemos ninguna idea previa de la frecuencia esperada, la estrategia más conservadora es realizar el cálculo asumiendo que la prevalencia esperada es del 50% (0,50). Para una misma precisión es la prevalencia que más tamaño muestral nos estimará, ya que el valor de p (1 - p) oscila de 0 a 1, con un valor máximo cuando p = 0,5.

El otro elemento que hay que conocer es la precisión o diferencia que hay que estimar. Esta precisión también requiere conocer el fenómeno estudiado, pero, generalmente, es el investigador el que establece la precisión en función de ciertos factores, de los que destacamos tres:

• La existencia de estimaciones de referencia con las que se quiere comparar.
• La estimación de la diferencia clínicamente importante.
• La disponibilidad o factibilidad del equipo investigador para reclutar sujetos.

Imaginemos que tratamos de estimar la prevalencia de obesidad en una población escolar de un área desfavorecida. Si tenemos la impresión de que esta población tiene una mayor prevalencia de obesidad que la población general, la precisión de nuestra estimación la obtendremos de la diferencia entre la prevalencia de la población general y la que nosotros creemos va a tener la población desfavorecida. Si existe información publicada de que en la población general hay un 18% de obesidad y esperamos encontrar una prevalencia entre la población desfavorecida de al menos un 25%, la precisión requerida será la diferencia entre ambas cifras: 7%. En la calculadora introduciremos el 25% esperado y el ±7% de precisión que buscamos.

El segundo factor que hay que considerar es la “diferencia clínicamente importante”. Usando el ejemplo anterior, si no podemos intuir cuál es la prevalencia en la población desfavorecida, tendremos que establecer qué diferencia de prevalencia consideraríamos suficiente para tener “importancia clínica”. En este ejemplo, parece sensato asumir que una diferencia de prevalencia de obesidad de al menos el 5% es clínicamente importante, ya que supone un aumento relativo del 27% de la prevalencia (0,05 / 0,18 = 0,27), lo que puede tener impacto en la salud cardiovascular de la población.

El tercer factor, la factibilidad, condiciona en la práctica muchas estimaciones de tamaño muestral. Con frecuencia, el investigador tiene limitaciones de reclutamiento para alcanzar determinados tamaños muestrales, por lo que cae en la tentación de restringir sus objetivos de precisión. Si el cálculo de tamaño muestral supera su capacidad de reclutamiento, no es excepcional que se busquen objetivos menos precisos. Así, si una precisión de ±5% implica un tamaño muestral inaccesible, se explora el tamaño necesario para otros objetivos, por ejemplo, 7% o 10%. Debemos advertir que esta actitud resulta poco rigurosa, ya que cuando el objetivo de precisión necesario es del 5%, si no somos capaces de reclutar la muestra requerida, lo más razonable es renunciar a realizar el estudio o bien buscar la colaboración de otros grupos de investigación con los que ampliar el reclutamiento.

En proyectos que precisan la aprobación de un comité ético de investigación o que optan a becas de investigación, la estimación del tamaño muestral es uno de los principales factores a considerar, ya que informa a los evaluadores de la factibilidad y relevancia del proyecto. Por ello, toda información que aportemos para justificar la estimación del tamaño muestral y la relevancia de la magnitud de los resultados a obtener es primordial.

Como hemos dicho anteriormente, aunque podríamos hacer los cálculos de tamaño muestral a partir de las fórmulas del error estándar, no lo recomendamos. Es preferible dedicar más nuestra atención a los parámetros que debemos utilizar para su cálculo que al proceso matemático. Existen diversas calculadoras epidemiológicas, muchas de ellas de fácil manejo y de acceso gratuito, unas para ejecución en línea (por ejemplo, Granmo, Powerandsamplesize.com) y otras para su instalación en ordenadores personales (por ejemplo, Ene, Epidat, GPower, PS) y dispositivos móviles (por ejemplo, n4Studies).

Para este documento vamos a realizar la estimación de tamaño muestral con la calculadora Granmo, disponible para su ejecución online en varios idiomas (https://www.imim.cat/ofertadeserveis/software-public/granmo/). La aplicación permite calcular el tamaño muestral para estimaciones de proporciones, medias, tiempos de supervivencia y coeficientes de correlación. Para proporciones y medias ofrece opciones de comparaciones de grupos independientes y apareados, y cálculos de potencia de un contraste estadístico. Asimismo, en el menú de proporciones hay dos opciones para estimaciones de riesgos relativos y odds ratios. Para ilustrar el procedimiento abordaremos a continuación dos escenarios: la estimación de una proporción poblacional y la comparación de dos proporciones independientes.

Estimación de una proporción poblacional

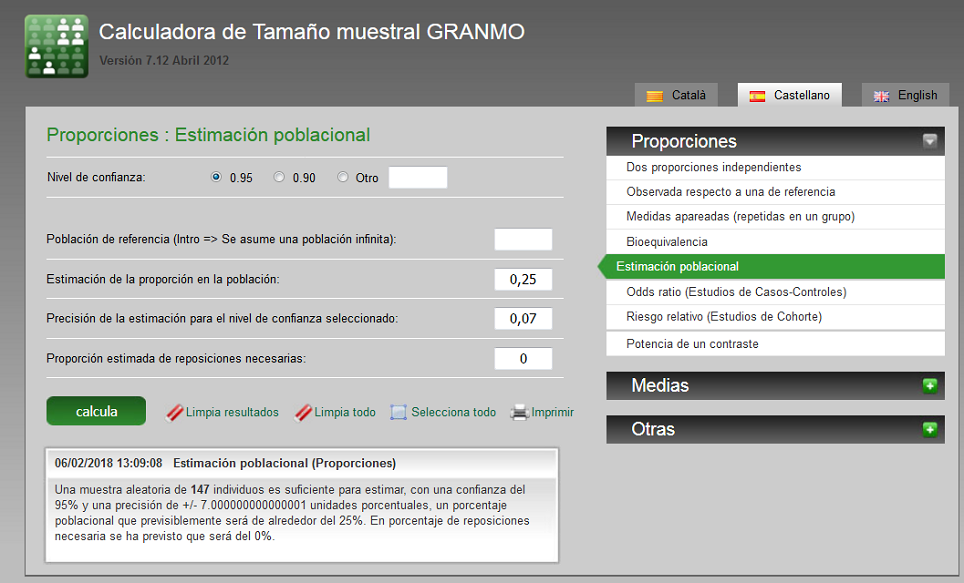
Comenzaremos con el ejemplo anteriormente mencionado de estimación de una proporción. Recordemos: prevalencia esperada de obesidad 25%, con una precisión de ±7%. Cuando accedemos al programa, la opción que por defecto aparece es la comparación de dos proporciones independientes (en la versión en castellano, menú “Proporciones” y opción “Dos proporciones independientes"); para nuestro ejemplo debemos seleccionar la opción “Estimación poblacional”. En la figura 2 se reproduce la pantalla correspondiente con los datos necesarios ya incorporados.

Figura 2. Cálculo del tamaño muestral para una estimación de una proporción con Granmo. Mostrar/ocultar

Disponible en https://www.imim.cat/ofertadeserveis/software-public/granmo/

Hemos dejado en blanco la casilla destinada a la población de muestreo disponible (si la población del área desfavorecida es limitada, debe introducirse aquí, para ajustar el tamaño muestral a la población disponible) y a 0 el porcentaje de reemplazo (podríamos haber puesto aquí el porcentaje esperado de pérdidas para compensarlas en la estimación del tamaño muestral). Recordamos que este programa pide proporciones (de 0 a 1), no porcentajes. Cuando hemos insertados todos los datos, accionamos el botón “Calcula” y el programa nos indica que se necesitan 147 sujetos.

Comparación de dos proporciones independientes

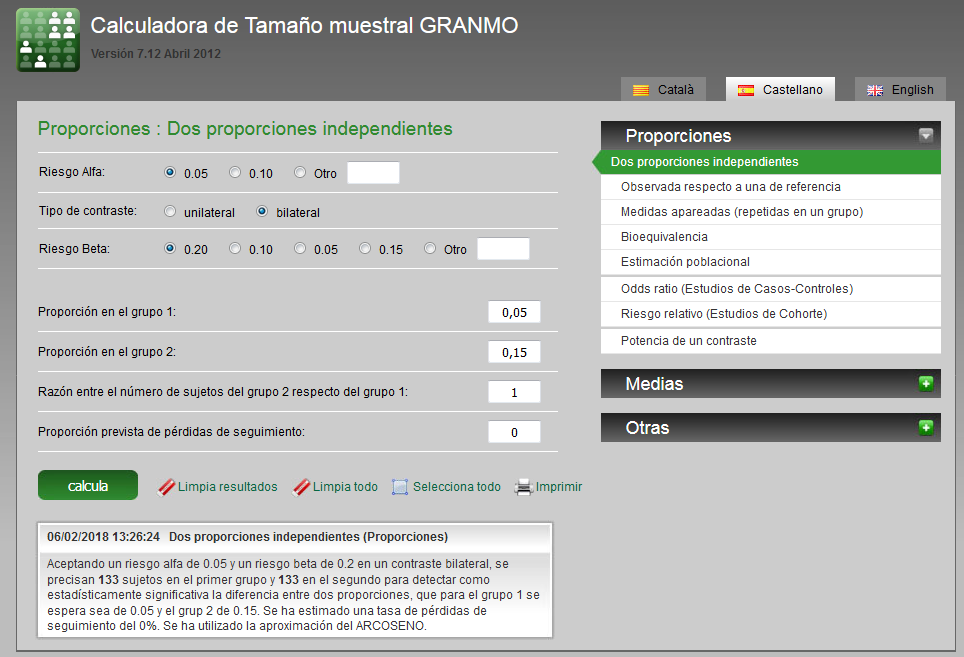
Para la estimación del tamaño muestral de una comparación de proporciones, emplearemos los datos de un estudio que trata de encontrar una diferencia de al menos el 10% en el riesgo de necesitar ventilación mecánica invasiva, de dos grupos de recién nacidos con distrés respiratorio por aspiración meconial, tratados con presión positiva continua en la vía respiratoria (CPAP) nasal u oxígeno en campana (proporciones esperadas respectivas del 5 y el 15%). En la figura 3 se presenta el cálculo de tamaño muestral.

Figura 3. Cálculo del tamaño muestral para una diferencia de proporciones con Granmo. Mostrar/ocultar

Disponible en https://www.imim.cat/ofertadeserveis/software-public/granmo/

Además de las proporciones esperadas, debemos indicar la relación entre los grupos (si los grupos son de igual tamaño muestral introduciremos “1”, si el grupo 2 debe tener el doble de sujetos introduciremos “2”) y la proporción esperada de pérdidas (si no prevemos pérdidas introduciremos “0”). Por defecto, el programa asigna otros parámetros ya abordados en documentos previos de esta serie:

• Riesgo alfa (error tipo I).
• Riesgo beta (error tipo II).
• El tipo de contraste (unilateral o bilateral).

Recordaremos que el riesgo alfa es la probabilidad de que encontremos diferencias cuando no las hay (error tipo I o de falso positivo) y el riesgo beta la probabilidad de que no encontremos diferencias cuando sí las hay (error tipo II o de falso negativo). Se acepta que el máximo riesgo alfa asumible es 0,05 (5%) y el máximo riesgo beta asumible es 0,20 (20%). Cuanto más exigentes seamos en el umbral de error (riesgos menores), mayor será la muestra necesaria.

El tipo de contraste depende de la hipótesis que planteemos en el estudio; si nuestra hipótesis considera las dos colas de la distribución normal (hipótesis de diferencia) o solo una (hipótesis solo de superioridad o solo de inferioridad). El tipo de contraste elegido se traduce en que el factor que multiplicará el error estándar será, para un error tipo I del 5%, 1,96 (Z_α/2 bilateral) o 1,65 (Z_α unilateral), por lo que el contraste bilateral siempre implicará un mayor tamaño muestral.

Como vemos en la figura 3, el programa asigna, por defecto, un riesgo alfa de 0,05; un riesgo beta de 0,20 y un contraste bilateral. La estimación de tamaño muestral es de 133 sujetos en cada grupo.

Bibliografía

• Altman DG, Bland JM. Statistics notes: the normal distribution. BMJ. 1995;310:298.
• Altman DG, Bland JM. Statistics notes: variables and parameters. BMJ. 1999;318:1667.
• Altman DG. Practical statistics for medical research. Londres: Chapman & Hall; 1991.
• Campbell MJ, Julious SA, Altman DG. Estimating sample sizes for binary, ordered categorical and continuous outcomes in two groups comparisons. BMJ. 1995;311:1143-8.
• Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Inferencia estadística: probabilidad, variables aleatorias y distribuciones de probabilidad. Evid Pediatr. 2019;15:27.
• Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Inferencia estadística: contraste de hipótesis. Evid Pediatr. 2020;16:11.
• Ochoa Sangrador C, Ortega Páez E, Molina Arias M. Inferencia estadística: estimación por intervalos. Evid Pediatr. 2019;15:40.
• Rosner B. Fundamentals of Biostatistics. 7.ª edición. Boston: Brooks/Cole, Cengage Learning; 2011.

Cómo citar este artículo

Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Inferencia estadística: estimación del tamaño muestral. Evid Pediatr. 2020;16:24.