Inferencia estadística

En artículos previos de esta serie dijimos que la estadística es una herramienta que nos ayuda a tomar decisiones en presencia de incertidumbre. Nuestro objetivo es estimar parámetros de la población a partir de la información obtenida en muestras. Esta estimación va a estar siempre asociada a una mayor o menor incertidumbre, por muy grande que sea el tamaño de la muestra que estudiemos. También diferenciamos entre la estadística descriptiva y la inferencia estadística. Dijimos que la inferencia estadística es el objetivo principal de la estadística, ya que es la que nos permite cuantificar nuestra incertidumbre.

Dentro de la inferencia estadística diferenciamos dos tipos de estrategias:

• La estimación de intervalos de confianza, que nos informa del rango de valores entre los que se encontrará el parámetro poblacional que hay que estimar.
• El contraste de hipótesis, con el que habitualmente confrontamos dos o más alternativas, cuantificando la probabilidad de que las diferencias entre ellas se deban al azar.

Veamos un ejemplo. En un ensayo clínico se compararon dos tratamientos, A y B, en dos grupos de 100 pacientes, para prevenir recaídas de una enfermedad. En el grupo A recayeron un 20%, mientras que en el grupo B un 40%. Podemos hacer una estimación de la eficacia de los tratamientos de dos maneras:

• Mediante estimación de intervalos de confianza: podemos decir que el tratamiento A es un 20% mejor que el tratamiento B (40-20%) y que estimamos, con un 95% de confianza (grado de error admitido de un 5%), que dicha diferencia se encuentra entre un 7,6% y un 32,4%. Todos los valores del intervalo son favorables al tratamiento A (no hay valores negativos), por lo que nos puede servir para tomar decisiones. A la hora de interpretar un intervalo de confianza, debemos fijarnos si incluye el valor nulo, que implica la ausencia de efecto (el "0" para las diferencias o el "1" para los cocientes); en este caso vemos que el cero no está incluido en el intervalo, luego las diferencias serán estadísticamente significativas.
• Mediante contraste de hipótesis: podemos decir que el tratamiento A es mejor que el B, con una probabilidad de error de 0,002 (estimación realizada mediante comparación de proporciones con aproximación a la normal). Como el error es menor del 5%, asumimos que el tratamiento A es mejor. Veremos más adelante que el contraste de hipótesis implica la formulación de hipótesis nula y alternativa, sobre las que se estima la probabilidad de error y, en función de la magnitud de error, podemos o no rechazar la hipótesis nula (no hay diferencias) y aceptar la alternativa (el tratamiento A es mejor que el B).

Debemos advertir que los fundamentos en los que se basan los análisis del ejemplo anterior no han sido todavía abordados en esta serie de artículos, aunque no es necesario conocer los procedimientos de cálculo subyacentes para entender los distintos abordajes de la inferencia estadística.

Probabilidad, variables aleatorias y distribucionesd de probabilidad

Uno de los objetivos habituales de la investigación es estimar la frecuencia de una determinada característica, por ejemplo, la presencia o no de obesidad. Si nuestro estudio tiene suficientes sujetos, por ejemplo, estudiamos a una muestra representativa de 10 000 adolescentes de nuestra comunidad y encontramos 1800 obesos, la frecuencia relativa de obesidad (1800/10 000 = 0,18) es la mejor aproximación que tenemos a la probabilidad de estar obeso en nuestro medio. La probabilidad no solo se refiere a variables nominales dicotómicas, también se puede aplicar a cualquier otro tipo de variable; por ejemplo, puede interesarnos saber la probabilidad de que un diabético tenga una glucemia precomida entre 70 y 150 mg/dl.

Podemos definir probabilidad como un número entre 0 y 1, asociado con la verosimilitud de que ocurra un suceso (número de casos favorables/número de casos posibles). Asumiendo una muestra de tamaño suficientemente alta (infinita) esta probabilidad se estimaría con la frecuencia relativa.

A partir de esta estimación de probabilidad podemos decir que cada uno de nuestros adolescentes tiene una probabilidad de 0,18 (18%) de ser obeso. Siguiendo terminología propia de la teoría de la probabilidad, cada adolescente es un experimento aleatorio, del que antes de explorarlo sabemos que puede o no ser obeso (posibles resultados del experimento) y la probabilidad de cualquiera de ellos (obeso p = 0,18), pero hasta que no lo exploramos no sabemos si lo es.

Las variables se caracterizan por ser fruto de observaciones repetidas de una misma característica, su información fundamental se puede resumir en un listado de los diversos resultados posibles y en la frecuencia (probabilidad) con que aparece cada uno de ellos. Lo habitual es que la probabilidad de cada uno de los valores de una variable siga algún tipo conocido de distribución de probabilidad. Existen muchas distribuciones de probabilidad, probablemente la más conocida sea la distribución normal, que siguen los valores de muchas variables continuas (por ejemplo, la talla de los adolescentes).

Cuando los distintos valores de una variable siguen una distribución de probabilidad la denominamos variable aleatoria. Para definir una variable aleatoria necesitamos conocer los valores posibles y la probabilidad de que ocurra cada uno de ellos. Veamos dos ejemplos. La variables aleatoria "curación de un tipo de tumor"; valores posibles: sí/no, distribución de probabilidad: binomial, probabilidad de curación 0,75 (75%). La variable aleatoria "longitud de los recién nacidos a término"; valores posibles: cualquier valor entre 40-60 cm, distribución de probabilidad: normal con media 50 cm y desviación típica 2 cm.

Al elegir una variable, asumimos un tipo concreto de distribución de probabilidad, que condicionará las estimaciones y contrastes de hipótesis que queramos realizar con ella. A cada valor o rango de valores de una distribución de probabilidad le corresponde una probabilidad; esta relación se determina por lo que conocemos como función de probabilidad (también llamada función de masa para distribuciones discretas y función de densidad para distribuciones continuas).

Existen múltiples distribuciones de probabilidad. Algunas ya han sido mencionadas, como la distribución binomial, para variables nominales dicotómicas, o la distribución normal, para variables continuas, pero hay muchas otras, como la distribución de Poisson (eventos raros que tienen lugar a lo largo de un periodo de tiempo o espacio), χ² (que siguen los valores observados y esperados de una tabla de contingencia), t de Student (que siguen las medias o diferencias de medias de muestras de pequeño tamaño), F de Snedecor (que siguen los cocientes de varianzas), etc.

Invitamos al lector interesado a profundizar su conocimiento de las distribuciones de probabilidad en los textos mencionados en la bibliografía.

Por su interés, abordaremos las características de la distribución normal, ya que nos permitirá presentar la relación existente entre los valores de una distribución y su probabilidad.

La distribución normal

La distribución normal (o gaussiana o acampanada) es la distribución continua más ampliamente utilizada. Constituye la piedra angular de la mayor parte de los métodos de estimación y contraste de hipótesis, por la asunción de que las variables aleatorias siguen una distribución normal.

La distribución normal puede ser aplicada no solo a variables con distribución esencialmente normal, sino también a variables de distribución no normal adecuadamente transformadas o a estimaciones de parámetros poblacionales de otras variables aleatorias (por ejemplo, proporción de obesos) realizadas a partir de los datos de muestras con un tamaño suficiente (en función del teorema central del límite n ≥30).

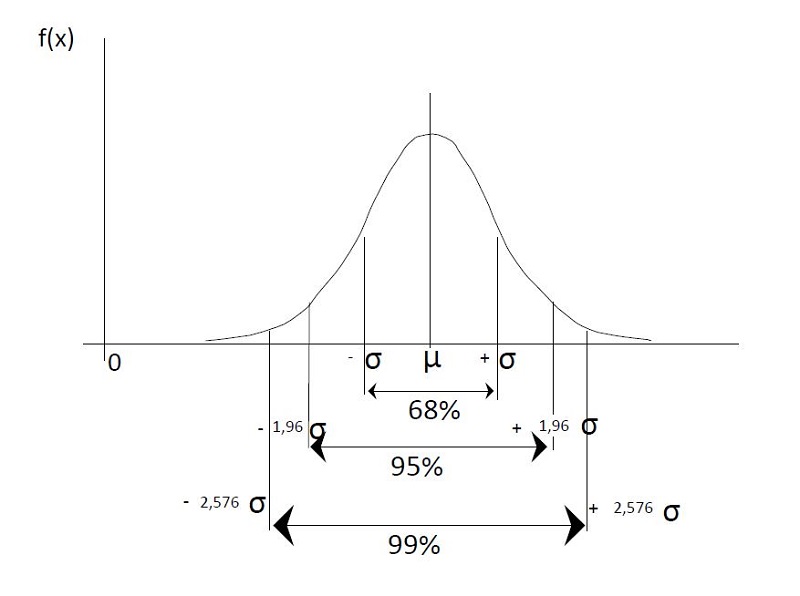
La distribución normal viene caracterizada por su simetría, por su valor central (μ, valor esperado, media o esperanza matemática) y por su dispersión proporcional a la varianza (σ², varianza). Nos basta con conocer la media y la varianza para estimar la probabilidad de cualquier rango de valores. Así, sabemos que a cada lado de la media se sitúa el 50% de los valores, que entre la media menos y más una unidad de desviación típica (raíz cuadrada de la varianza) se encuentran el 68% de los valores y que entre la media menos y más 1,96 veces la desviación típica el 95% de los valores (figura 1).

Figura 1. Distribución de probabilidad normal. Mostrar/ocultar

Repasemos; la distribución normal es:

• Centrada y simétrica a los dos lados de la media (50% de los valores a cada lado de la media).
• Rango media ±1 desviación típica: 68% de los valores.
• Rango media ±1,96 veces la desviación típica: 95% de los valores.

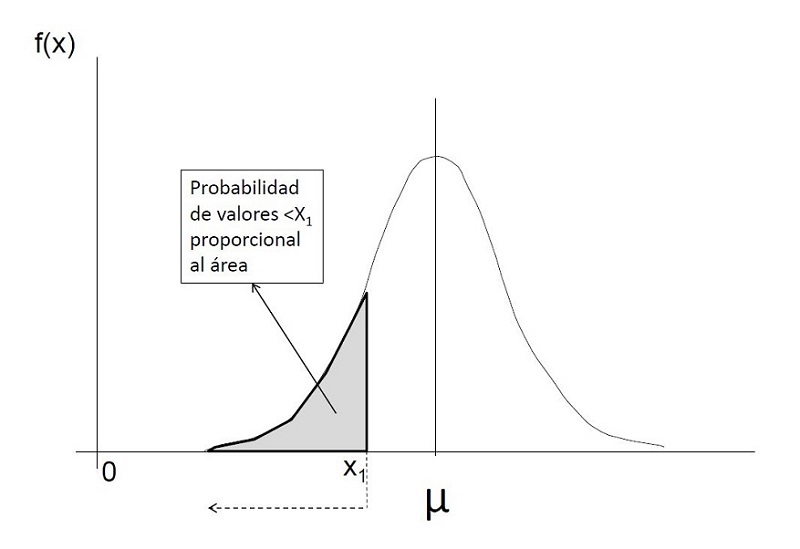
Además de esos valores de referencia, contamos con tablas de referencia detalladas de probabilidades para cada unidad de desviaciones típicas, no solo de forma simétrica, sino además asimétricas (a una o dos colas o lados del valor) (figura 2). Así, sabemos que el valor que corresponde a la media menos 1,65 veces la desviación típica deja a su izquierda el 5% de los valores.

Figura 2. Rango de valores de una distribución normal. Mostrar/ocultar

Hemos dicho que, conociendo la media y la desviación típica de una variable de distribución normal, podemos conocer la probabilidad de cualquier rango de valores; por ejemplo, en la distribución de longitudes de recién nacidos a término, de media 50 cm y desviación típica 2 cm (representada con la nomenclatura "N(50,2)"), podemos saber la probabilidad de que un recién nacido nazca con menos de 46 cm. Como 46 corresponde a la media menos dos veces (casi 1,96 veces) la desviación típica (50 - [2 × 2] = 46), podemos calcular sin necesitar más información la probabilidad de medir menos de 46 cm, que es aproximadamente 0,025 (un 2,5%, ya que fuera del intervalo ±1,96 veces la desviación típica quedaba el 5% y aquí solo contamos un lado).

El cálculo exacto a partir de funciones de probabilidad requiere operaciones complejas, que son innecesarias, ya que tanto las hojas de cálculo como los paquetes estadísticos tienen memorizados los valores de referencia que corresponden a cada valor de una distribución de referencia que denominamos normal estandarizada o tipificada (Z), creada a partir de una transformación, que consiste en restar a cada valor la media (centrar) y dividirlo por la desviación típica (estandarizar o tipificar).

$$ Z = \frac{X - μ}{σ}$$

La distribución de referencia "Z" tiene una media 0 y una desviación típica 1 (representada con la nomenclatura "N(0,1)"). En la figura 3 representamos a la derecha la distribución muestral original de longitudes de recién nacidos a término, de media 50 y desviación típica 2, y a la izquierda la distribución normal estandarizada "Z", de media 0 y desviación típica 1. Ambas distribuciones son equivalentes en cuanto a probabilidad. Si queremos calcular la probabilidad de valores menores o mayores de un determinado valor real basta con calcular el valor correspondiente Z, restándole la media (centrar) y dividiéndolo por la desviación típica (estandarizar). La probabilidad de Z en las tablas de referencia será la probabilidad del valor real. En la figura 3 se presenta la estimación para una longitud de recién nacido 45 o menor. Con la centralización y estandarización podemos estimar la probabilidad de cualquier valor que siga una distribución normal, si sabemos la media y la desviación típica.

Figura 3. Distribución normal (longitud de recién nacidos a término) de media "50" y desviación típica "2" y distribución normal estandarizada (Z) de media "0" y desviación típica "1". Mostrar/ocultar

También se puede hacer el paso inverso, saber a qué valor real de longitud de recién nacido le corresponde una probabilidad concreta, buscando el valor de la normal estandarizada (Z) al que le corresponde dicha probabilidad y haciendo la transformación inversa: multiplicar por la desviación típica y sumar la media. Esta operación se representa como:

$$ P = Φ(Z) ⟹ X = (Z * σ) + μ $$

Algunos de los valores Z ya se han mencionado al describir la distribución normal, ya que son los factores que multiplicaban la desviación típica para delimitar el 68% o el 95% de los datos a ambos lados de la media (1 y 1,96 respectivamente) o bien el 95% a un solo lado (1,65).

El resto de los valores de referencia de Z pueden ser consultados en tablas disponibles en los textos de referencia, aunque no suele ser necesario consultarlos, porque la mayoría de los programas estadísticos facilitan la probabilidad asociada al valor Z resultante.

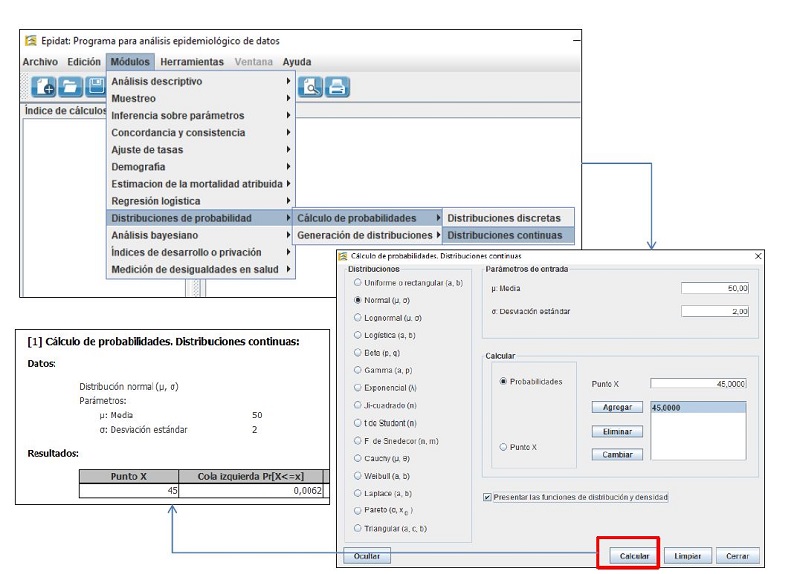
Podemos familiarizarnos con el cálculo de probabilidades asociado a los valores de una distribución de probabilidad utilizando calculadoras estadísticas. Recomendamos usar la que contiene el programa Epidat 4.2, software gratuito que puede ser descargado libremente (https://www.sergas.es/Saude-publica/EPIDAT-4-2?idioma=es) y que no requiere instalación (el fichero descargado se puede ejecutar).

En el menú "Módulos > Distribuciones de probabilidad > Cálculos de probabilidad > Distribuciones continuas" podemos elegir la distribución normal. Nos pedirá la media y desviación típica de nuestra distribución y el valor real, para el cual queremos estimar la probabilidad. En la figura 4 se presentan la pantalla con los datos y los resultados. En una distribución normal de media 50 y desviación típica 2, un valor de 45 o menor tiene una probabilidad de 0,0062 (0,62%).

También podemos hacer el paso inverso, a partir de una probabilidad, el programa puede darnos el valor real que delimita esa probabilidad; para ello elegiremos la opción "Punto X" en vez de "Probabilidad".

Cuando no disponíamos de los paquetes informáticos actuales, el cálculo de estos valores precisaba de la estandarización previa, ya que habitualmente solo teníamos las tablas de valores correspondientes a la distribución normal estandarizada N(0,1). Con los programas actuales este paso ya no es necesario. Sin embargo, nuestro conocimiento de las características de la distribución normal hace más fácil comprender, sin necesidad de cálculos, si nos encontramos ante sucesos con menor o mayor probabilidad de ocurrir. Volviendo al ejemplo anterior, no es fácil hacerse una idea de la probabilidad de que un recién nacido mida menos de 45 cm, aun conociendo la media y la desviación típica. Sin embargo, en una distribución normal estandarizada es más fácil comprender que la probabilidad de estar por debajo de -2,5 desviaciones estándar es muy baja. Otro ejemplo de la utilidad de esta distribución de referencia es lo que conocemos como "puntuación Z" (z-score en inglés), para expresar magnitudes de peso, talla o índice de masa corporal en relación con la edad y sexo de un paciente pediátrico.

Distribuciones de probabilidad e inferencia estadística

El mismo fundamento visto para la distribución normal se aplica para variables aleatorias que siguen otras distribuciones de probabilidad conocidas, tanto discretas como continuas. Si conocemos cómo se distribuyen los valores posibles de estas otras variables podemos estimar la probabilidad de un valor encontrado o de un rango de valores.

Como veremos en próximos artículos de esta serie, también las estimaciones de parámetros poblacionales obtenidas de muestras aleatorias de la población siguen alguna de las distribuciones de probabilidad conocidas. Cuando realizamos un estudio en una muestra, nuestra muestra solo es una de las posibles muestras que podríamos haber seleccionado a partir de la población. Por lo tanto, nuestra muestra nos proporcionará una estimación puntual (por ejemplo, media, proporción, diferencia de medias, diferencia de proporciones, etc.), que será solo una de las múltiples estimaciones puntuales teóricas que hubiéramos obtenido con otras muestras. Si estas estimaciones teóricas siguen alguna distribución de probabilidad conocida, podremos estimar su precisión (intervalo de confianza) y hacer contrastes de hipótesis. La distribución de probabilidad de estas estimaciones puntuales va a depender del tipo de variable, del tamaño muestral, de su magnitud y, para variables continuas, de otros parámetros descritos en la muestra (por ejemplo, desviación típica). Con estos parámetros calcularemos los estadísticos de referencia, equivalentes al valor Z que vimos para la distribución normal, a los que les corresponderá una probabilidad, que podemos consultar en tablas o que directamente nos dará el programa estadístico. También podremos hacer el paso inverso, encontrar el valor o rango de valores que corresponde a una probabilidad; esto nos servirá, por ejemplo, para calcular entre qué valores se encontrarán el 95% de las estimaciones teóricas, lo que corresponde al intervalo de confianza del 95%.

En la figura 4 vemos las principales distribuciones de probabilidad continuas. Entre ellas, se encuentran algunas de las más frecuentemente utilizadas, como la distribución de χ², la t de Student y la F de Snedecor. La distribución de Ji-cuadrado, es la que siguen las diferencias entre valores esperados y observados de una tabla de contingencia y la emplearemos cuando realicemos un test de χ². La distribución t de Student, es la que siguen las diferencias de medias, por lo que la emplearemos cuando hagamos una comparación de medias, con un test de la t de Student. La distribución F de Snedecor es la que siguen los cocientes de varianzas, por lo que la emplearemos cuando hagamos un análisis de la varianza.

Figura 4. Módulo de Epidat 4.2 para cálculo de probabilidades de distribuciones continuas. Mostrar/ocultar

Igualmente hay distribuciones de probabilidad de variables discretas, como la distribución binomial y la hipergeométrica, que emplearemos en pruebas exactas, como el test exacto de Fisher, o la distribución de Poisson que describe la ocurrencia de eventos raros en intervalos de tiempo o espacio, que resulta muy útil para estimar intervalos de frecuencias de enfermedades poco frecuentes.

En nuevos artículos de esta serie repasaremos los fundamentos y procedimientos de la inferencia estadística, revisando la estimación de intervalos de confianza y el contraste de hipótesis.

Bibliografía

• Altman DG, Bland JM. Statistics notes: the normal distribution. BMJ. 1995;310:298.
• Altman DG, Bland JM. Statistics notes: variables and parameters. BMJ. 1999;318:1667.
• Altman DG. Practical statistics for medical research. Londres: Chapman & Hall; 1991.
• Milton JS. Estadística para biología y ciencias de la Salud. México: McGraw-Hill; 2001.
• Norman GR, Streiner DL. Bioestadística. México: Mosby/Doyma Libros, 1996.
• Ochoa Sangrador C, Molina Arias M. Estadística. Tipos de variables. Escalas de medida. Evid Pediatr. 2018;14:29.
• Rosner B. Fundamentals of Biostatistics. 7.ª edición. Boston: Brooks/Cole, Cengage Learning; 2011.

Cómo citar este artículo

Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Inferencia estadística: probabilidad, variables aleatorias y distribuciones de probabilidad. Evid Pediatr. 2019;15:27.