En estadística inferencial existen dos tipos de pruebas estadísticas que difieren en cuanto a la referencia que tomemos en el contraste de hipótesis, las pruebas paramétricas y las no paramétricas. Las paramétricas, tratadas en capítulos anteriores, se basan en la comparación de un parámetro, como la media, una distribución de datos, conocida de antemano, como la distribución normal o la t de Student; estas pruebas precisan muestras de un tamaño suficientemente grande y datos que no presenten una asimetría exagerada. En las pruebas no paramétricas, la distribución de los datos no es conocida de antemano y no está sujeta a ninguna distribución de probabilidad, de ahí que algunos las denominen pruebas libres de distribución. El contraste de hipótesis no está basado en ningún parámetro, se fundamentan en la comparación del orden que presentan los datos, no están sujetas a un determinado tamaño muestral y funcionan bien cuando la asimetría de los datos o su distribución no se aproxima a una distribución normal.

De forma general, las pruebas no paramétricas comparten unas características comunes:

• Los datos se distribuyen de forma aleatoria e independiente en las muestras, salvo en los datos pareados.
• Tienen pocas restricciones y asunciones en cuanto a la distribución de la población.
• La variable dependiente o es ordinal o se puede ordenar en rangos.
• El análisis se realiza por el ordenamiento en rangos.
• Las hipótesis se realizan sobre rangos, medianas o frecuencias de los datos.
• Se pueden realizar incluso con tamaños de muestra pequeños.

Presentan una serie de ventajas:

• Se pueden aplicar siempre, ya que tienen pocos supuestos.
• Cuando no se satisfacen los supuestos de la prueba paramétrica, son más efectivas que estas.

Presentan una serie de desventajas:

• Existe una pérdida de información al trabajar con rangos y no con toda la muestra, tanto si se cumplen como si no se cumplen los supuestos de normalidad.
• Son menos potentes que las pruebas paramétricas si los puestos de normalidad se cumplen.
• No se pueden calcular intervalos de confianza de forma directa, hay que recurrir al remuestreo o bootstrapping.

Aunque existen muchas pruebas no paramétricas, en este capítulo veremos las más frecuentemente utilizadas en Ciencias de la Salud.

Prueba no parámetrica para comparar la tendencia central poblacional de una muestra

Queremos conocer si un determinado valor, normalmente la mediana, pertenece a una población de referencia. En este caso se utiliza la prueba de Wilcoxon de los rangos con signo para una muestra. Es el sustituto de la prueba de comparación de una media con la población de referencia, cuando la distribución de los datos de nuestra muestra no se puede aproximar a una distribución normal. El contraste de hipótesis se realiza bajo la hipótesis nula de la igualdad de las medianas, con la hipótesis alternativa de que las medianas no son iguales. La prueba se realiza calculando el valor absoluto de la resta de cada observación menos la mediana con la que queremos contrastar, se ordenan de mayor a menor y se les asigna un rango o número de orden. Se suman los rangos de las diferencias positivas (aquellas que el valor observado es mayor que la mediana) y de las negativas (aquellas que el valor observado es menor que la mediana). Si la hipótesis nula fuera cierta, ambas diferencias serán muy parecidas. Se contrasta si la probabilidad del estadístico de menor valor de la suma de rangos (V) es menor que la debida al azar.

Veamos un ejemplo utilizando un programa de acceso libre, el software estadístico R (https://www.r-project.org/) con el plugin RCommander (https://www.rcommander.com/) y la base de datos fundam_no_param.RData (tabla 1), disponible en la web de Evidencias en Pediatría). Si necesita saber cómo instalar RCommander, puede consultar el siguiente tutorial en línea (http://sct.uab.cat/estadistica/sites/sct.uab.cat.estadistica/files/instalacion_r_commander_0.pdf).

Tabla 1. Base de datos fundamentos no paramétricos. Mostrar/ocultar

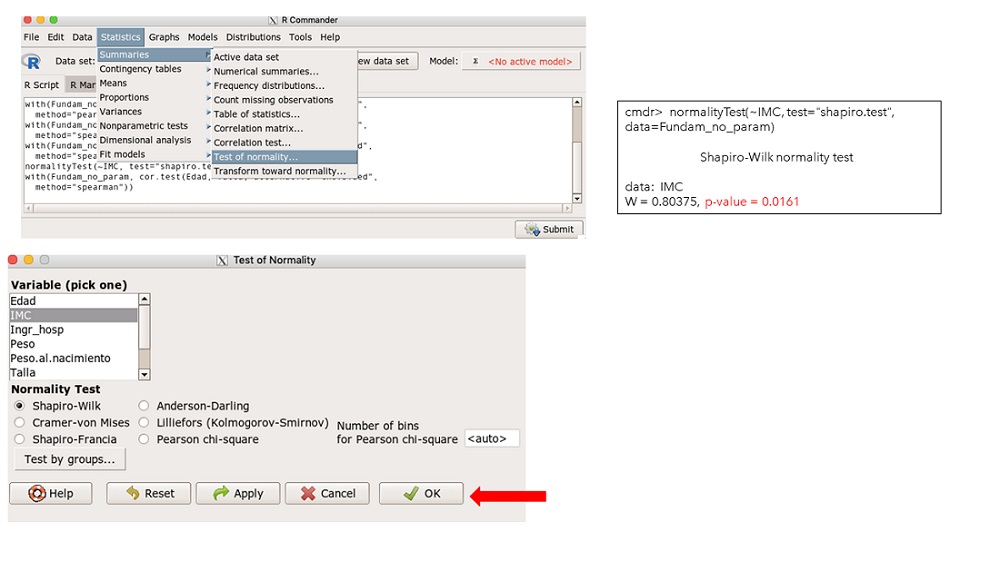
Tomemos como ejemplo la variable índice de masa corporal (IMC). Queremos conocer si los datos de nuestra muestra pertenecen a la población de referencia. Sabemos que la mediana de nuestra muestra es 16,16 kg/m² y la mediana de población general es 18 kg/m². En primer lugar, debemos conocer si nuestros datos pueden acercarse a una distribución normal, para ello realizamos el test de normalidad de Shapiro-Wilk que es el recomendado para muestras pequeñas (<50). En el menú de RCommander seleccionamos las opciones Statistics (Estadísticos)\Summaries (Resúmenes)\Test of normality (test de normalidad)… y, en la ventana emergente, marcamos la variable “IMC”, elegimos Shapiro-Wilk y pulsamos el botón OK (figura 1). En la ventana de resultados vemos que la p es menor de 0,05 (p = 0,01619), por tanto, rechazamos la hipótesis nula de normalidad.

Figura 1. Prueba de normalidad IMC. Mostrar/ocultar

Al no cumplirse la normalidad de la distribución, tenemos que recurrir a una prueba no paramétrica, en este caso la prueba de Wilcoxon de los rangos con signo. Para ello, en la ventana de RCommander seleccionamos Statistics (Estadísticos)\No parametrics test (Test no paramétricos)\Single sample Wilcoxon-test (test para una muestra de Wilcoxon)… en la siguiente ventana seleccionamos “IMC” en “Data” y en “options” (opciones) introducimos en mu (valor de la mediana) = 18, two-sided (bilateral), ya que la hipótesis nula es de igualdad y en “Type of test” (tipo de test) elegimos “exact” (exacto), para conocer la probabilidad exacta (recomendada) (figura 2). En la ventana de resultados R nos muestra, en primer lugar, la media (16,16) y la mediana (17,47), seguidamente el tipo de prueba: bilateral y exacta, seguida del estadístico de contraste (V), la probabilidad: p = 0,32; también nos indica la hipótesis alternativa de que la mediana es distinta de 18. Al ser la p >0,05 no podemos rechazar la hipótesis nula de igualdad de medianas, luego nuestros datos pueden pertenecer a la población de referencia (figura 2).

Figura 2. Prueba de Mann-Whitney para una muestra. Mostrar/ocultar

Prueba no parámetrica para comparar la tendencia central de dos muestras

Existe en la literatura confusión en la nomenclatura de esta prueba. Podemos encontrarla como prueba de U de Mann-Whitney, prueba de los rangos de Wilcoxon para dos muestras independientes o bien prueba de Mann-Whitney-Wilcoxon. Las dos se basan en la ordenación de los datos y en la utilización de rangos para realizar el contraste, pero el estadístico es diferente (la U en la de Mann-Whitney, la W en la de Wilcoxon), aunque los resultados en cuanto a nivel de significación son equivalentes.

Se debe de aplicar como sustituto de la prueba de comparación de medias para dos muestras (t de Student) cuando:

• El tamaño muestral de algunos de los grupos es menor de 30 y la distribución de los datos no puede aproximarse a la distribución normal.
• Cuando la variable independiente es ordinal.
• Si la muestra es muy pequeña (≤10).

Son un 5% menos potentes que la t-Student cuando la distribución se puede aproximar a la normal, sin embargo, en muestras muy asimétricas y en tamaños muestrales pequeños son más robustas. Tienen la desventaja de que los intervalos de confianza, aunque posibles, son difíciles de realizar.

Las condiciones de aplicación en las dos son las mismas:

• Las muestras deben ser independientes entre sí.
• La variable dependiente puede ser continua u ordinal y la independiente nominal dicotómica.
• No precisan de una distribución conocida para su aplicación. Esto hace que se puedan aplicar siempre y que sean especialmente útiles como alternativa a los test paramétricos o cuando las muestras son muy pequeñas.
• Aunque no es imprescindible la igualdad (homocedasticidad) de las varianzas, la prueba funciona mejor si las varianzas son iguales, ya que las muestras se diferencian solo en su tendencia central y el contraste se realiza entre las medianas. En caso contrario la dispersión de las muestras hace que no se pueda garantizar el contraste de las medianas, realizándose entre la probabilidad de que alguna localización de uno de los grupos sea distinta respecto al otro, perdiéndose potencia. En este último caso hay que tener mucha precaución en la interpretación de la probabilidad resultante.

Prueba de los rangos con signo de Wilcoxon para dos muestras independientes

Tomemos como ejemplo en la base de datos fundam_no_param.RData, la comparación entre el IMC y el tabaquismo familiar.

Comprobemos las condiciones de aplicación. En primer lugar, vemos que las dos muestras son independientes entre sí, los padres fumadores son distintos a los no fumadores. Segundo, la variable dependiente (IMC) es continua y se pueden asignar rangos u orden y la variable independiente (tabaquismo) es nominal dicotómica (sí/no). La distribución de los datos de IMC en ambas categorías no sigue una distribución normal, lo comprobamos por la prueba de Shapiro-Wilk con una p = 0,043 (<0,05) en el grupo de fumadores (figura 3) y por la forma de la distribución de los datos en los no fumadores según el histograma de densidades con la curva normal superpuesta (figura 4). Por último, comprobamos la homocedasticidad de las varianzas por la prueba ya vista en el capítulo de comparación de medias, obtenemos una p = 0,1488 (>0,05) lo que significa que no podemos rechazar la hipótesis nula de igualdad de varianzas.

Figura 3. Prueba de normalidad entre IMC y tabaquismo. Mostrar/ocultar

Figura 4. Gráfico de densidad para comprobación de normalidad entre IMC y tabaquismo. Mostrar/ocultar

La prueba se realiza ordenando los valores de los dos grupos de menor a mayor, asignando un rango u orden a cada uno de ellos. Posteriormente sumamos los rangos de cada grupo obteniendo los estadísticos de contraste W₁ (grupo 1) y W₂ (grupo 2). La prueba contrasta, de forma bilateral, que la probabilidad de que un resultado de la muestra primera (PA) supere a la segunda (PB) es la misma de que la segunda (PB) supere a la primera (PA), lo que es lo mismo que los valores en una muestra no sean mayores que los de la otra muestra. Cuando las varianzas son iguales el contraste se realiza entre las medianas (la probabilidad de uno de los grupos es mayor de 0,5), en caso contrario se realiza por la totalidad de las probabilidades de cada grupo. La hipótesis alternativa es que alguna probabilidad de ambas muestras supere a la otra.

$$ H_0: P(A>B)=P(B>A)\space \space\space\space \space\space\space H_1 :P(A>B) ≠ P(B>A)$$

$$ H_0: P(A>B)=0,5\space\space\space\space\space\space H_1 :P(A>B) ≠ 0,5 $$

En la práctica, para conocer el nivel de significación de la prueba, basta con contrastar si el valor más bajo de la suma de rangos es excesivamente bajo como para atribuirlo al azar en una tabla tabulada para la prueba de Wilcoxon. El nivel crítico de decisión de las tablas es unilateral, multiplicando por 2 obtendremos la probabilidad bilateral.

En nuestro caso, en la tabla 2 representamos los valores de las dos categorías de la variable tabaquismo (sí/no) ordenadas de menor a mayor. A la derecha se representan los rangos asignados a cada categoría con las sumas de los rangos correspondientes a la categoría SI (W₁ = 48) y a la categoría NO (W₂ = 7). Contrastando el menor valor de la suma de rangos (W₁) en la tabla de Wilcoxon, obtenemos una p = 0,0167 (unilateral) y bilateral (2 × 0,0167) p = 0,0334. Como la p <0,05, concluimos que existen diferencias significativas entre la distribución entre el IMC de los niños respecto a la condición de fumar o no fumar de los padres.

Tabla 2. Prueba de Wilcoxon-Mann Whitney para dos muestras independientes. Mostrar/ocultar

Prueba de la U de Mann-Whitney para dos muestras independientes

El principio es el mismo que la prueba de Wilcoxon, se ordenan los valores de menor a mayor y se asignan rangos, pero el estadístico de contraste es la U de MannWhitney, que es el valor mínimo de U₁, U₂, que se obtienen de la siguiente forma:  

$$U_1= n_1n_2\space +\frac {n_1 (n_1+1)}{ 2 } - W_1; \space U_2= n_1n_2\space +\frac {n_2 (n_2+1)}{ 2 } - W_2;$$

donde n₁, n₂, son los tamaños muestrales de cada grupo y W₁ y W₂ son las sumas de rangos de cada grupo. El contraste se realiza con el valor más bajo de la U resultante en la tabla de Mann-Whitney para los dos tamaños muestrales correspondientes. Al igual que la prueba de Wilcoxon el nivel de significación es unilateral.

Aplicándolo a nuestro ejemplo anterior:

$$ U_1= n_1n_2\space +\frac {n_1 (n_1+1)}{ 2 } - W_1= 7*3 +\frac {7 (7+1)}{ 2 }-48=1 $$

$$ U_2= n_1n_2\space +\frac {n_2 (n_2+1)}{ 2 } - W_2= 7*3 +\frac {3 (3+1)}{ 2 }-7=20. $$

Contrastando el menor valor U₁=1 en la tabla tabulada de Mann-Whitney obtenemos una p = 0,1167 unilateral, lo que corresponde a 0,0334 bilateral. Como podemos observar son resultados idénticos a los de la prueba de los rangos de Wilcoxon.

RCommander, aunque la denomina prueba de Wilcoxon para dos muestras independientes, lo que realmente hace es el contraste con la U de Mann-Whiney.

Veamos cómo se realiza en R. En la base de datos antes comentada, nos vamos a la pestaña de Statistics (Estadísticos)\No parametrics test (Test no paramétricos)\Two-sample Wilcoxon test (test de Wilcoxon para dos muestras)… en la ventana emergente en la pestaña de “Data” seleccionamos la variable dependiente en “Groups” (Grupo) tabaquismo, en “Response Variable” (variable explicada) IMC. En la pestaña “Options” (opciones), elegimos “two-sided” (bilateral) y “exact” (Exacto), damos a OK. En la ventana de salida de datos obtenemos las dos medianas de cada grupo, la comparación bilateral, el contraste entre IMC y tabaquismo, la prueba que estamos realizando (Wilcoxon Rank sum exact test), el estadístico de contraste, la U de Mann-Whitney, que R lo llama W = 1 y la p = 0,0333, exactamente igual que la realizada anteriormente de forma manual. Al final nos informa que la hipótesis alternativa es que la verdadera localización de la diferencia de los valores es distinta de 0 (en este caso, la diferencia de medianas es distinta de 0). Como conclusión tenemos, que el IMC presenta valores más elevados de forma significativa (p = 0,033) en los niños con padres fumadores que en los no fumadores (figura 5).

Figura 5. Prueba de Mann-Whitney para dos muestras independientes. Mostrar/ocultar

Vemos pues que, aunque con estadísticos de contrastes distintos, ambas pruebas, la de Wilcoxon y Mann-Whitney, ofrecen resultados idénticos, la elección depende del paquete estadístico que usemos. Se recomienda en general, utilizar la prueba de la U de Mann-Whitney porque es la más usada por los paquetes estadísticos y para diferenciarla de la Wilcoxon para muestras emparejadas.

RCommander no nos ofrece el Intervalo de confianza de las diferencias de las medianas, si estamos interesados en conocerla se puede realizar mediante comandos de sintaxis. Basta con introducir en la consola de R Commander: wilcox.test (IMC~Tabaquismo, conf.int=TRUE) y el programa nos devuelve el intervalo de confianza del 95% (IC 95): -11,9 a -0,009, que no incluye el valor nulo (0), por lo tanto, rechazamos la hipótesis nula de igualdad entre los dos grupos.

Prueba no paramétrica de tendencia central para comparar K muestras. prueba de Kruskall-Wallis

Es la generalización de la prueba de U de Mann-Whitney para comparar más de dos (K) grupos independientes. No se precisa que las distribuciones de los grupos en cada categoría sigan una distribución normal ni homogeneidad de las varianzas. Es la prueba sustituta no paramétrica del análisis de la varianza (ANOVA) cuando las variables son ordinales, el tamaño de la muestra es pequeño, no existe normalidad en los residuales y las varianzas de los grupos son muy heterogéneas. Presenta el inconveniente de que es menos potente (menos probabilidad de encontrar diferencias cuando en verdad existen) que el ANOVA, si se cumplen los supuestos de esta, y no permite la construcción de intervalos de confianza de forma directa. Al igual que la prueba de Mann-Whitney, se ordenan de menor a mayor las observaciones y se les asigna un rango a cada una. La hipótesis nula es que la probabilidad en alguna localización (normalmente la mediana) en los tres grupos sea la misma.

Veamos un ejemplo. En nuestra base de datos, elegimos la variable Gravedad.asma codificada como ordinal (leve-moderado-grave) y el IMC. Queremos saber si el IMC influye de alguna manera en la gravedad del asma. En primer lugar, realizamos la prueba de normalidad, como ya conocemos, entre la variable IMC y Gravedad.asma (figura 6) y obtenemos una p = 0,01235 en la categoría de asma moderado. Al no seguir una distribución normal y tener un tamaño muestral muy pequeño debemos recurrir a una prueba no paramétrica.

Figura 6. Prueba de normalidad entre IMC y Gravedad.asma. Mostrar/ocultar

En RCommander vamos al menú Statistics (Estadísticos)\No parametrics test (test no paramétricos)\Kruskall-Wallis test (test de Kruskall-Wallis)… y en la siguiente ventana elegimos Gravedad.asma en “Groups” (Grupos), IMC en “Response variable” (variable explicada) y pulsamos OK (figura 7). En la ventana de resultados observamos las medianas de las tres categorías que claramente son mayores en el grupo grave (18,94), siendo muy parecidas en las de leve (15,14) y moderado (15,55), con una p = 0,018 (<0,05). Se interpreta como que existen diferencias estadísticas significativas en el IMC en función de la gravedad del asma. RCommander no nos ofrece contrastes a posteriori, como en el ANOVA, por lo que no es posible saber si existen diferencias significativas entre las variables comparadas dos a dos, aunque intuitivamente parece que en el asma grave el IMC es mucho mayor.

Figura 7. Prueba de Kruskall-Wallis entre IMC y Gravedad.asma. Mostrar/ocultar

Correlacion no parámetrica de los rangos de Spearman

Como ya se comentó en el artículo anterior, es el sustituto de la correlación lineal de Pearson cuando no se cumple el supuesto de normalidad de las variables, el tamaño muestral es muy escaso o las variables son ordinales y la relación entre las mismas es monótona (las dos variables aumentan o disminuyen en el mismo sentido y con una tendencia constante).

Se representa por el coeficiente de correlación de Spearman (r_s) que es estimador del parámetro poblacional ρ (rho). Nos mide la fuerza de asociación o relación entre dos variables sin presuponer direccionalidad entre ellas. A mayor valor absoluto mayor correlación, siendo el 1 o -1 la correlación perfecta directa o inversa entre las variables y el 0, como valor nulo, la no existencia de correlación. Al ser r una estimación del coeficiente poblacional ρ, la prueba de hipótesis se debe plantear sobre la probabilidad de independencia de las variables a nivel poblacional. Así tendremos que H₀: ρ = 0 y H₁ρ ≠ 0.

Volviendo a nuestra base de datos, elegimos dos variables: la edad y la talla. Estamos interesados en conocer si existe correlación entre ambas. Comprobamos la normalidad de la distribución de ambas muestras (figura 8). Obtenemos que el IMC no sigue una distribución normal (p = 0,016), sin embargo, la talla sí se puede aproximar a una distribución normal (p = 0,19), en estos casos no es posible aplicar la correlación lineal porque la distribución normal deber ser bivariada, aplicamos entonces la de Spearman.

Figura 8. Comprobación de la normalidad en la correlación de Spearman. Mostrar/ocultar

En la pestaña de Rcommander Statistics (Estadisticos)\Summaries (Resúmenes)\Correlation test (test de correlación)…, en la siguiente ventana pulsamos en las dos variables IMC y edad, elegimos “Spearman Rank-order” (correlación de Spearman) y “two-sided” (bilateral) y pulsamos OK. En los resultados tenemos el coeficiente de correlación ρ = 0,31 y la significación estadística p = 0,37 (figura 9). La interpretación sería que existe una correlación mediana entre el IMC y la talla; sin embargo, esta no es significativa. Es importante reseñar que solo con el valor del coeficiente de correlación no basta, debemos realizar la prueba de hipótesis para obtener el nivel de significación, ya que nos podemos encontrar ante situaciones que pueden presentar correlación y esta no ser significativa.

Figura 9. Correlación no paramétrica de Spearman. Mostrar/ocultar

RCommander no facilita el intervalo de confianza, pero se puede calcular fácilmente por el argumento “spearman.ci” del paquete RVAideMemoire de R, como se detalla en el siguiente script:

>install (RVAideMemoire)

> library(RVAideMemoire)

> spearman.ci(IMC,Edad)

Obtenemos el IC 95 de ρ (-0,63 a 0,77), como incluye el valor nulo (0), podemos concluir que no es significativo.

Correspondencia de las pruebas no paramétricas

Hemos visto que cuando el supuesto de normalidad se vulnera, la comparación entre la tendencia central de 2 muestras emparejadas se realiza por la prueba de Wilcoxon y si son más de dos grupos se realiza por la Prueba de Friedman, sustitutas de la t de Student y de la ANOVA con medidas repetidas respectivamente. En la tabla 3 resumimos las pruebas expuestas y sus alternativas paramétricas.

Tabla 3. Resumen de las pruebas paramétricas y sus equivalentes no paramétricas. Mostrar/ocultar

Bibliografía

• Amat J. Test de Wilcoxon Mann Whitney como alternativa al t-test. En: Ciencia de datos [en línea] [consultado el 21/09/2021]. Disponible en: www.cienciadedatos.net/documentos/17_mann–whitney_u_test
• Arriaza Gómez AJ, Fernández Palacín F, López Sánchez MA, Muñoz Márquez M, Pérez Plaza S, Sánchez Navas S. Estadística Básica con R y R-Commander. Cádiz: Universidad de Cádiz; 2008.
• Doménech Massons JM. Métodos estadísticos en ciencias de la salud. Unidad didáctica 11: Comparación de dos medias: pruebas t. Barcelona: Signo; 1998.
• Doménech Massons JM. Métodos estadísticos en ciencias de la salud. Unidad didáctica 12: Comparación de varias medias análisis de la varianza. Barcelona: Signo; 1998.
• Molina Arias M, Ochoa Sangrador C, Ortega Páez E. Comparación de dos medias. Pruebas de la t de Student. Evid Pediatr. 2020;16:51.
• Molina Arias M, Ochoa Sangrador C, Ortega Páez E. Correlación. Modelos de regresión. Evid Pediatr. 2021;17:25.
• Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Inferencia estadística: contraste de hipótesis. Evid Pediatr. 2020;16:11.
• Sánchez-Villegas A, Martín-Calvo N, Martínez-González MA. Correlación y regresión lineal simple. En: Martínez MA, Sánchez-Villegas A, Toledo EA, Faulin A (eds.). Bioestadística amigable. 3.ª edición. Barcelona: Elsevier España; 2014. p. 269-326.
• Sentís J, Pardell H, Cobo E, Canela J. Manual de Bioestadística. Capítulo 13. Pruebas no paramétricas. 2.ª edición. Barcelona: Masson; 1995. p. 211-9.
• Toledo E, López del Burgo C, Sayón-Orea C, Martínez-González MA. Comparación de medias entre grupos. En: Martínez MA, Sánchez-Villegas A, Toledo EA, Faulin A (eds.). Bioestadística amigable. 3.ª edición. Barcelona: Elsevier España; 2014. p. 187-90.

Cómo citar este artículo

Ortega Páez E, Ochoa Sangrador C, Molina Arias M. Pruebas no paramétricas. Evid Pediatr. 2021;17:36.