Introducción

En un documento previo sobre análisis multivariante abordamos los fundamentos del análisis multivariante, los tipos de análisis y el proceso de modelización multivariante. Asimismo, mostramos este proceso para la regresión lineal múltiple. En este documento repasaremos el proceso para la regresión logística múltiple.

Regresión logística múltiple

La regresión logística es una técnica de análisis que utilizamos cuando se desea conocer la relación entre una variable dependiente cualitativa dicotómica y una o más variables explicativas independientes, ya sean cualitativas o cuantitativas. Existen variantes de esta técnica para cuando la variable dependiente es nominal politómica, esto es, tiene más de dos categorías (regresión logística multinomial o politómica), y para cuando es ordinal (regresión logística ordinal).

El objetivo de la regresión logística binaria no es, como en la regresión lineal, predecir el valor de la variable dependiente (Y) a partir de una o varias variables independientes (X), sino predecir la probabilidad de que ocurra el evento que caracteriza la variable dependiente (éxito, enfermedad, etc.), conocidos los valores de las variables independientes.

La variable dependiente va a adoptar los valores 1 y 0 que representan, respectivamente, la presencia y ausencia del evento que clasifica dicha variable. Para explorar la contribución de las variables independientes a la estimación de la probabilidad de la variable dependiente, tendríamos que construir un modelo similar al empleado en regresión lineal:

$$a\space+\space b_1X_1\space+\space b_2X_2\space +\space....\space +\space b_mX_m$$

Sin embargo, el resultado de esta ecuación no va a dar estimaciones de probabilidad (p) entre 0 y 1, porque para determinados valores de las variables independientes sus resultados podrán estar entre menos y más infinito. Para resolver este problema la regresión logística hace dos transformaciones. Primero, transforma cada probabilidad para cada combinación de valores de las variables independientes en sus odds (p/[1-p]), que adoptan valores entre cero e infinito. En segundo lugar, calculan los logaritmos neperianos de las odds, ln(p/[1-p]), que adoptan valores entre menos y más infinito y que además siguen una distribución lineal.

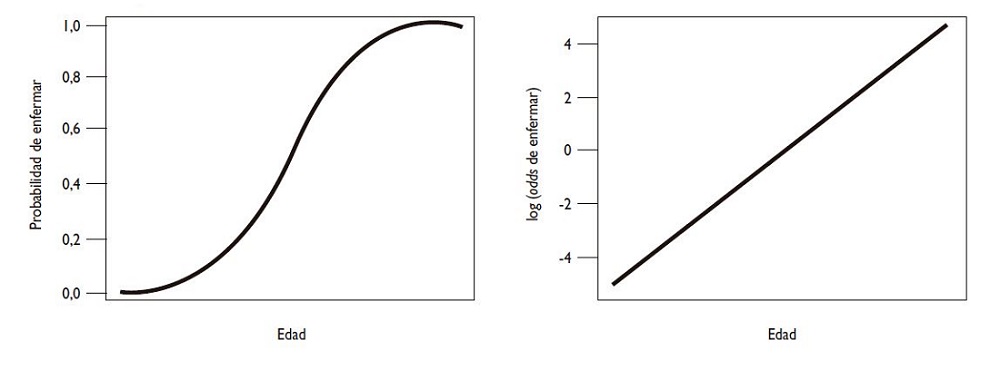
En la figura 1 se presentan las distribuciones de las probabilidades de enfermar en función de la edad, que siguen una distribución sigmoidea, y a su derecha las transformaciones en logaritmos naturales de las odds de dichas probabilidades, que siguen una distribución lineal.

Figura 1. Distribución de las probabilidades de enfermar en función de la edad y los logaritmos naturales de las odds de dichas probabilidades. Mostrar/ocultar

Con este nuevo parámetro ya podemos emplear una ecuación lineal. La fórmula de la regresión logística quedaría:

$$Ln(p/[1-p])\space=\space b_0\space +\space b_1X_1\space+ \space b_2X_2 \space +\space .... \space+ \space b_nXn$$

De la que podemos calcular directamente las probabilidades con la fórmula:

$$P(Y) = \frac {1}{1 \space + \space e^{-(b_0+b_1X_1+b_2X_2+....+b_nXn)}}$$

En la que P(Y) es la probabilidad de que Y adopte el valor 1 (éxito, enfermedad, etc.), b_o es la constante del modelo, b_i los coeficientes de cada variable independiente y X_i sus valores.

En la figura 2 se muestran funciones logísticas con sus correspondientes estimaciones de coeficientes. El punto de inflexión de la función, que corresponde habitualmente al valor de la variable con una probabilidad del 50% (0,50), determina la constante (a) y la pendiente de la tangente en ese punto el coeficiente de la variable (b). En la parte inferior de la figura se presentan una serie de funciones con los coeficientes estimados.

Figura 2. Funciones logísticas. Mostrar/ocultar

Las covariables cualitativas deben ser dicotómicas, tomando valor 0 para su ausencia y 1 para su presencia. Si la covariable tuviera más de dos categorías debemos realizar una transformación de la misma en varias covariables cualitativas dicotómicas ficticias (variables indicadoras o dummies). Luego veremos un ejemplo. Al hacer esta transformación, cada categoría de la variable entraría en el modelo de forma individual, aunque su modelización y análisis debe ser conjunto.

Aunque las covariables cuantitativas pueden ser analizadas en su escala natural, no siempre el riesgo asociado a cada unidad de la variable alcanza la magnitud suficiente para mostrar significación clínica o estadística. Por ello, no es infrecuente tener que recodificar estas variables para que el modelo estime el riesgo asociado a determinados rangos o magnitudes de la variable.

La interpretación de los coeficientes en la regresión logística es distinta que la de los coeficientes de la regresión lineal; aquí se utilizan para calcular las odds ratio (OR) ajustadas de cada variable, que se obtienen exponenciando el coeficiente (e^b); el cálculo es proporcionado habitualmente por los paquetes estadísticos. Esta OR equivale a la OR combinada que obtendríamos en un análisis estratificado.

Para ilustrar el procedimiento de la regresión logística vamos a realizar un análisis con los datos de una serie de casos de gastroenteritis aguda. Queremos construir un modelo para predecir la gastroenteritis bacteriana. En la figura 3 se presentan las frecuencias de gastroenteritis bacteriana en función de algunas variables seleccionadas: presencia de sangre en heces, edad menor de 2 años y estación del año.

Figura 3. Frecuencia de gastroenteritis bacteriana en función de la presencia de sangre en heces, edad menor de 2 años y estación del año. Mostrar/ocultar

Podemos observar que en presencia de sangre en heces es mucho más frecuente la gastroenteritis bacteriana, que aparentemente no hay diferencias por edades, aunque el riesgo asociado a sangre en heces parece tener lugar principalmente en los menores de 2 años. Asimismo, observamos que en verano es mucho más frecuente la presencia de gastroenteritis bacteriana. Como vemos, hay varias variables implicadas, por lo que parece necesario recurrir a análisis multivariante.

Los pasos de la modelización son:

1. Modelo máximo

   Incluimos las variables descritas en la figura 3, además de un término de interacción entre edad menor de 2 años y sangre en heces.

2. Codificación de variables y elección de los valores de referencia

   Todas las variables se han recodificado a valores 0-1 y hemos creado tres variables indicadoras (dummies) para analizar la estación del año, siguiendo el esquema de la tabla 1. Con este esquema cada una de las variables indicadoras, de valor 0 o 1, expresarán la diferencia de riesgo entre cada estación y la estación de referencia, en este caso invierno. En función del programa estadístico que empleemos, las variables indicadoras las tendremos que crear nosotros o las creará automáticamente el programa, pero siempre debemos controlar este proceso y conocer el esquema de recodificación, del que existen diversas alternativas, para poder interpretar los resultados. Asimismo, hemos creado un término de interacción para modelizar la diferente capacidad predictiva de la sangre en heces en función de la edad menor/mayor de 2 años (EdadxSangre), multiplicando los valores de ambas variables.

   Tabla 1. Recodificación de variables indicadoras (valores nuevos). Mostrar/ocultar

   	Valores originales de la variable estación del año
   Variables indicadoras	1 (invierno)	2 (primavera)	3 (verano)	4 (otoño)
   E_Primavera	0	1	0	0
   E_Verano	0	0	1	0
   E_Otoño	0	0	0	1

3. Estrategia de modelización

   Elegimos una estrategia “hacia atrás”, considerando el valor Z asociado a cada variable (contraste de Wald), estimado a partir del cociente de cada coeficiente y su error estándar. Hay que recordar que las variables indicadoras entran y salen del modelo en bloque, aunque individualmente algunas de ellas no resulten significativas. Asimismo, el término de interacción entra con las variables relacionadas, pero puede eliminarse, dejando las relacionadas, si no resulta estadísticamente significativo y su eliminación no empeora el modelo en conjunto.

   En la figura 4 se presenta el análisis de regresión logística múltiple realizado con RCommander. En la salida de resultados se presentan los coeficientes de cada variable (Estimate), sus errores estándar (Std. Error), el contraste individual (Z value) y su significación (Pr(>|z|)), más abajo están los coeficientes exponenciados (Exponentiated coefficients “odds ratios”) y sus intervalos de confianza. Los coeficientes de las variables indicadoras (Primav, Verano y Otoño) y sus correspondientes OR informan de la probabilidad de gastroenteritis bacteriana en comparación con el riesgo de la estación de referencia implícita (Invierno). Podemos ver que ingresar en verano se asocia a un riesgo 5,21 veces mayor que en invierno (categoría de referencia), con una confianza del 95% de que aumenta entre 2,25 y 12,97 veces. Aunque la presencia de sangre en heces está muy asociada a la etiología bacteriana, en este análisis se ve que solo es así en los menores de dos años. Como se comentó en el documento previo de análisis estratificado, los análisis deben darse por separado. En menores de dos años, el riesgo de tener bacterias en heces de los que tienen sangre en heces es 16,11 veces mayor que el de los que no la tienen; esta OR se calcula exponenciando la suma de los coeficientes de las variables Sangre en heces y la interacción (Exp[0,32 + 2,46]).

   Figura 4. Regresión logística para predicción de gastroenteritis bacteriana. Mostrar/ocultar

   

4. Evaluación de la fiabilidad del modelo

   Una vez desarrollado el modelo, el siguiente paso es evaluar su fiabilidad, estimando las medidas de bondad de ajuste, medidas que informan del ajuste de los datos predichos por el modelo a los datos observados reales. En la tabla 2 se presenta la salida correspondiente al modelo de la figura 4; incluye la tabla de clasificación de valores predichos y observados, que muestra una concordancia del 73,83%, y las estimaciones de la desviación (-2 logaritmo de la razón de verosimilitudes, en inglés deviance), y de los coeficientes de determinación R² (porcentaje de varianza explicada por el modelo). Ya comentamos para la regresión lineal múltiple la interpretación de R², que corresponde al porcentaje de varianza explicada por el modelo, que interesa sea lo mayor posible. Sin embargo, para la desviación nos interesa el modelo que la tenga menor, porque será el que mejor ajusta a los datos. Otro estimador proporcionado en el análisis es el criterio de información de Akaike (AIC), que ajusta la log-verosimilitud por el número de variables; resulta muy útil cuando hay muchas variables independientes; el mejor modelo será el que tenga el AIC más bajo.

   Tabla 2. Medidas de ajuste del modelo de regresión logística. Mostrar/ocultar

   GEA bacteriana	Valor predicho
   Valor observado	No	Sí	Porcentaje Correcto
   No	172	3	98,29
   Sí	64	17	20,99
   Acierto global			73,83

   -2 Log Verosimilitud 274,60
   R cuadrada de Cox & Snell 0,16
   R cuadrada de Nagelkerke 0,23

Aunque alguna de las variables presentan contrastes no significativos, no podemos prescindir de ellas, porque están vinculadas a otras variables indicadoras (primavera y otoño) o por sustentar el término de interacción (sangre en heces y edad menor de 2 años). Por ello, el modelo máximo elegido al inicio va a ser el modelo final.

Los modelos de regresión logística no tienen los requerimientos de los de regresión lineal. Así, no requieren que exista una relación lineal entre las variables dependiente e y las independientes, ni tampoco necesitan que haya normalidad ni homocedasticidad de los residuos. Sin embargo, sí requieren que la variable dependiente sea binaria (nominal dicotómica), que las observaciones sean independientes entre sí (no exista apareamiento o medidas repetidas) y que no exista colinealidad entre las variables independientes. Otro requisito es que los valores de las variables independientes tengan una relación lineal con los logaritmos de sus odds (probabilidad dividida por su complementario). También se requiere suficiente número de observaciones, al menos 10 eventos del resultado menos frecuente de la variable dependiente, por cada variable introducida en el modelo.

Bibliografía

• Abraira V, Pérez de Vargas Luque A. Métodos multivariantes en bioestadística. Ed. Centro de Estudios Ramón Areces. Madrid 1996.
• Arezina R, Duolao W. Source and control of bias. En: Duolao W, Bakhai A (eds.). Clinical trials. A practical guide to design, analysis and reporting. Londres: Remédica; 2006. p. 55-64.
• Argimón Pallás JM, Jiménez Villa J. Métodos de investigación clínica y epidemiológica. Barcelona: Elsevier, 2006.
• Molina Arias M, Ochoa Sangrador C, Ortega Páez E. Correlación. Modelos de regresión. Evid Pediatr. 2021;17:25.
• Molina Arias M, Ochoa Sangrador C, Ortega Páez E. Regresión lineal simple. Evid Pediatr. 2021;17:46.
• Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Métodos de ajuste de sesgos. Análisis estratificado. Evid Pediatr. 2022;18:31.
• Ortega Páez E, Ochoa Sangrador C, Molina Arias M. Regresión logística binaria simple. Evid Pediatr. 2022;18:11.
• Rosner B. Fundamentals of Biostatistics, 7th Edition. Boston: Brooks/Cole, Cengage Learning 2011.
• Rothman K. J. Epidemiología Moderna. Madrid: Díaz de Santos, 1987.
• Woodwark M. Epidemiology study design and data analysis. London; Chapman & Hall/CRC, 1999.

Cómo citar este artículo

Ochoa Sangrador C, Molina Arias M, Ortega Páez E. Regresión logística múltiple. Evid Pediatr. 2023;19:34.